Математика \ Математика

Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии, страница 3

>0, если векторы - правая тройка

=0, если векторы компланарны

<0, если векторы – левая тройка.

Необходимое и достаточное условие принадлежности четырех точек к одной плоскости имеет вид: 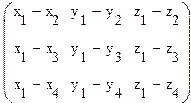   =   0, где координаты точек .

Аналитическая геометрия

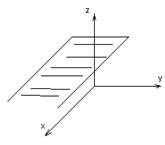
Плоскость

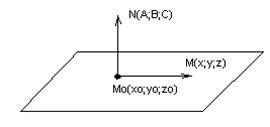
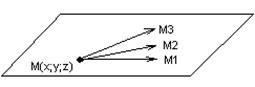
Составим уравнение плоскости, проходящей через

Вектор N называется нормалью к плоскости.

  -  уравнение плоскости. Проходящей через данную точку перпендикулярной данному вектору.

   -   общее уравнение плоскости

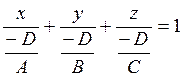
1)  y=0, z=0, x=a

2)  x=0, z=0, y=b

3)  x=0, y=0, z=с

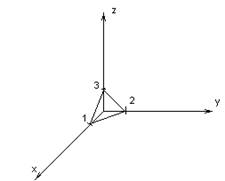
a, b, с – это отрезки, отсекаемые плоскостью на координатных осях.

Пример:

Дана плоскость: 2x+3y-4z-2=0

1)  Построить плоскость

2)  Найти отрезки. Отсекаемые на осях

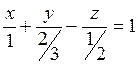
Плоскость отсекает отрезки: 1, 2/3, -1/2

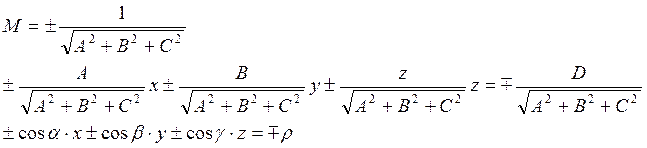
Знак нормирующего модуля М выбирают таки образом чтобы знак  был положительным.

  -   уравнение плоскости в нормальном виде.

 - расстояние от 0 до плоскости, если:

1)  D=0, то плоскость проходит через начало координат.

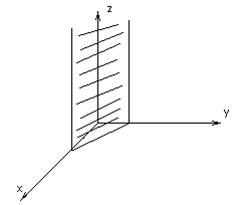
2)  С=0,

Плоскость пойдет параллельно оси 0z.

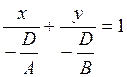
3)  A=0

Плоскость пойдет параллельно оси 0x.

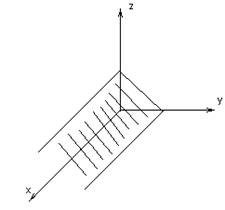
4)  B=0

Плоскость пойдет параллельно оси 0y.

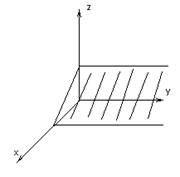
5)  Ax+D=0

Плоскость пойдет параллельно оси 0yz.

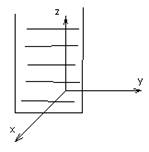
6)  By+D=0

Плоскость пойдет параллельно оси x0z

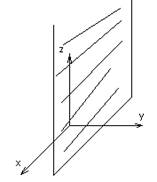
7)  Cz+D=0

Плоскость пойдет параллельно оси xy0

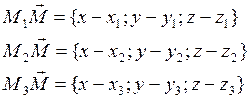
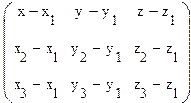
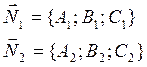
1)  Плоскости параллельны:

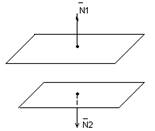
2) совпадающие плоскости:

3) Плоскости пересекаются:

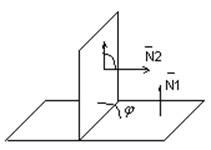
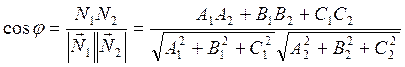
4)

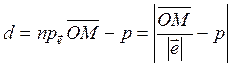
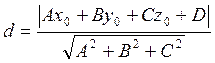
Пример: Найти расстояние т плоскости до т. Мо.

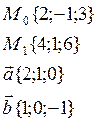
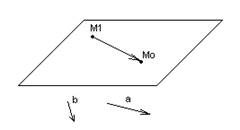
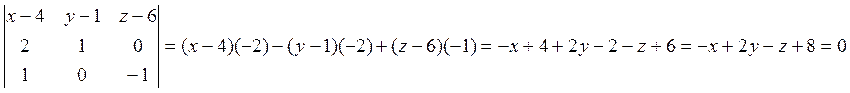
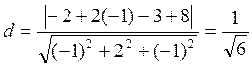
Прямая на плоскости.

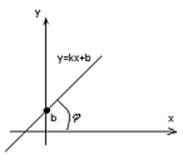
b – отрезок, отсекаемый прямой OY

1)

2) Уравнение прямой с заданным к, проходящим через заданную т.Мо(хо;уо)

   -   уравнение прямой

3)

4)

  или

 - не существует

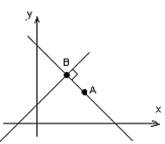
Пример: Найти проекцию т.А на прямой

А(1;2)

=

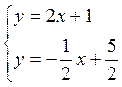
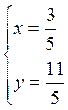
   - общее уравнение прямой       на плоскости

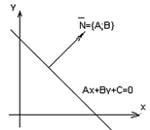
р - расстояние от прямой до 0

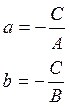
Пример: Привести уравнение  с угловыми коэффициентами.

                   

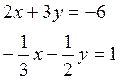
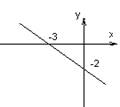
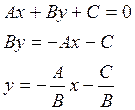
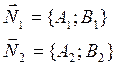
Прямые параллельны, когда

Прямые совпадают, если

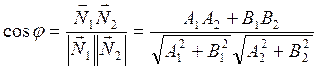
Условия перпендикулярности : 

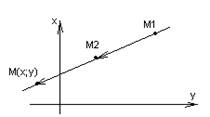
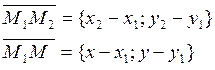
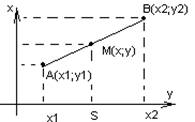
Деление отрезка в заданном соотношении

Отношение, по которому т.М делит отрезок АВ называется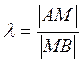

Пример: Найти координаты т.М, которая должна делить отрезок АВ в отношении .

Если M – середина, то

Прямая в пространстве.

1)  Канонические уравнения прямой

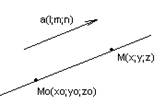
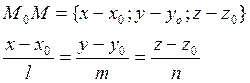
а – направляющий вектор

2)  Параметрические уравнения

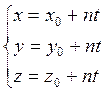
3)  Уравнение прямой через две точки

4)  Пересечение двух плоскостей

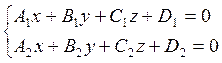
Пусть z = 0

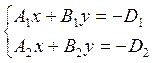
Пример: Привести уравнение прямой к каноническому виду.

Пусть у = 0

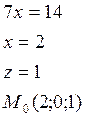
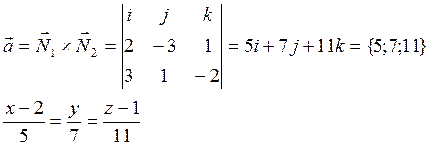
Взаимное положение прямых в пространстве

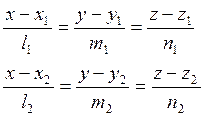
1)          -   условия параллельности прямых (колинеарности)

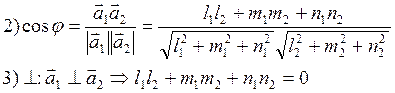 - При условии что прямые лежат в одной плоскости

Условия принадлежности двух непараллельных прямых одной плоскости имеет вид:

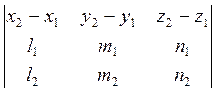 Через две прямых всегда можно провести одну плоскость.

 

1)  Прямая параллельна плоскости:

а)       

б)        Прямая лежит в плоскости:

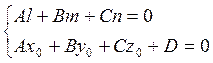
2)  Прямая пересекается плоскостью:

a)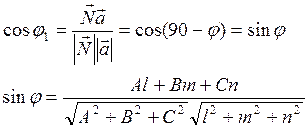

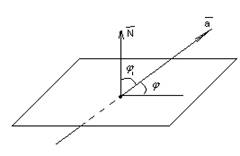
б) Прямая перпендикулярна плоскости:

Кривые второго порядка

   (1)   

, где числа А, В и С – не все равны 0.

1.         Определение:            Окружностью называется геометрическое место точек, равноудаленных от данной точки называемой центром окружности.

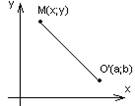
т.М принадлежит окружности, если

Каноническое уравнение окружности с центром  и радиусом R.

 

Теорема: Всякое уравнение (1) с В=0 и А=С описывает окружность или мнимую окружность .

Доказательство:

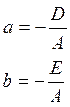
1)           - нормальное каноническое уравнение окружности

2)         = 0

Остается только

3)           - фигура – мнимая окружность.

2.  Определение:            Эллипсом называется геометрическое место точек, сумма расстояний которых до двух заданных точек, называемых фокусами, есть величина постоянная.

Скачать файл