Производная показательно-степенной функции.
Определение: Показательно-степенной
функцией называется функция вида ![]() , то есть функция, у
которой и основание и показатель степени являются функциями от х.
, то есть функция, у
которой и основание и показатель степени являются функциями от х.
Пример:
1) ![]()
![]()
2) ![]()
![]()
Теорема: ![]() (формула №19)
(формула №19)
Доказательство: ![]()
![]()
![]()
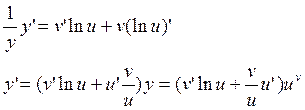
Пример: ![]()
![]()
![]()
![]()
Прием дифференцирования применяется для больших производных или дробей.
Пример: 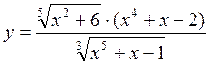
Логарифмируем: ![]()
Дифференцируем: 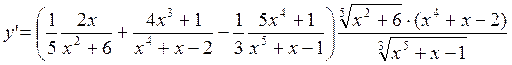
Производная обратной функции.
Замечания: Если ![]() непрерывна на отрезке
непрерывна на отрезке ![]() при чем
при чем ![]() и
и ![]() , то обратная функция определена и
непрерывна на отрезке
, то обратная функция определена и
непрерывна на отрезке ![]() .
.
Теорема: Если для функции ![]() существует функция
существует функция ![]() , которая в т. у имеет производную
, которая в т. у имеет производную ![]() , отличную от нуля, то в соответствии в
т. х функция имеет производную, вычисляемую по формуле:
, отличную от нуля, то в соответствии в
т. х функция имеет производную, вычисляемую по формуле: ![]()
Теорема: ![]() (формула №20)
(формула №20)
Доказательство: ![]()
![]()
![]()
![]()
![]()
Теорема: ![]() (формула №21)
(формула №21)
Доказательство: ![]()
![]()
![]()
![]()
![]()
Теорема: ![]() (формула №22)
(формула №22)
Доказательство: ![]()
![]()
![]()
Теорема: ![]() (формула №23)
(формула №23)
Пример: ![]()
1) Если ![]() правостороннее произведение.
правостороннее произведение.
2) Если ![]() левостороннее произведение.
левостороннее произведение.
3) Если ![]() , то функция в этой точке не
дифференцируема.
, то функция в этой точке не
дифференцируема.
Функция ![]() дифференцируема
на
дифференцируема
на ![]() ,
, ![]()
![]()
![]()
1. ![]()
![]() и
и ![]() - одного порядка малости.
- одного порядка малости.
2. ![]() имеет высший порядок малости.
имеет высший порядок малости.
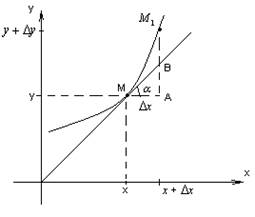
Таким образом приращение функции состоит из двух слагаемых первого и более высокого порядков малости.
Дифференциалом первого порядка
функции ![]() называется линейная относительно
называется линейная относительно ![]() часть приращение этой функции.
часть приращение этой функции.
![]()
![]()
![]()
![]()
![]() -
дифференциал независимой переменной х совпадает с его приращением
-
дифференциал независимой переменной х совпадает с его приращением ![]() .
.
![]() , то
есть производную можно рассматривать как
, то
есть производную можно рассматривать как 
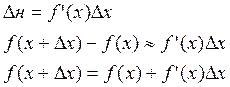
Пример: Вычислить ![]()
![]()
![]()
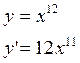
![]()
![]()
1) ![]()
2) ![]()
3) ![]()
![]()
![]()
![]()
Пусть ![]() и
и ![]()
![]()
![]()
Дифференциал сложной функции
имеет тот же вид, как и в случае, если ![]() было
независимой переменной (инвариантность форм дифференциала). Форма дифференциала
не зависит от того, является ли аргумент функции независимой переменной или
функцией другого аргумента.
было
независимой переменной (инвариантность форм дифференциала). Форма дифференциала
не зависит от того, является ли аргумент функции независимой переменной или
функцией другого аргумента.
![]()
![]() :
: ![]()
![]()
Дифференциал ![]() функции
функции ![]() ,
соответствующий данным значениям
,
соответствующий данным значениям ![]() и
и ![]() , равен приращению ординаты касательной
к графику функции
, равен приращению ординаты касательной
к графику функции ![]() в т. х.
в т. х.
Производные и дифференциалы высших порядков.
Производная от производной называется второй производной или производной второго порядка.
Производная ![]() -го порядка от функции
-го порядка от функции ![]() называется производная от производной
называется производная от производной ![]() -го порядка.
-го порядка.
![]()
Пример: ![]()
![]()
![]()
1. ![]()
![]()
![]()
![]()
2. ![]()
![]()
Дифференциал функции есть функция от х, причем от х зависит только первый сомножитель.
Второй сомножитель – приращение независимой переменной х.
Дифференциал от дифференциала функции называется вторым дифференциалом.
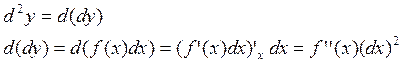
Дифференциалом ![]() -го порядка называется дифференциал от
дифференциала
-го порядка называется дифференциал от
дифференциала ![]() -го порядка.
-го порядка.
Если х является функцией другого аргумента, то последняя формула неверна, то есть второй и последующие дифференциалы свойством инвариантности не обладают. Производная от функции задана параметрически.
![]()
Параметрическое задание окружности.
![]()
![]()
Пусть функция ![]() имеет обратную функцию
имеет обратную функцию ![]() и пусть функции
и пусть функции ![]() и
и
![]() дифференцируемы по
дифференцируемы по ![]() , тогда
, тогда ![]() дифференцируема
по х.
дифференцируема
по х.
![]()
![]()
![]()
![]() (формула №24)
(формула №24)
![]() (формула №25)
(формула №25)
![]() (формула №26)
(формула №26)
Пример:
![]()
![]()
![]()
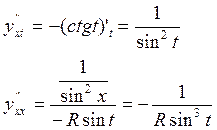
Некоторые теоремы о дифференцируемых функциях.
Теорема Роля: Если
функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и дифференцируема во всех его
внутренних точках и на концах отрезка
и дифференцируема во всех его
внутренних точках и на концах отрезка ![]() , то
существует, по крайней мере, одна т. С, производная которой обращается в 0.
, то
существует, по крайней мере, одна т. С, производная которой обращается в 0.![]()
Доказательство: ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то она достигает наибольшего
, то она достигает наибольшего ![]() и наименьшего
и наименьшего ![]() значений.
значений.
1) ![]()
![]()
![]()
![]()
2) ![]()
![]() хотя бы одно из них не 0, пусть
хотя бы одно из них не 0, пусть ![]() .
.
Пусть функция принимает свое наибольшее значение в некоторой т. С
![]() , так
как
, так
как ![]() ,
, ![]()
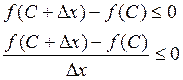
![]() ,
при
,
при ![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.