Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии, страница 4

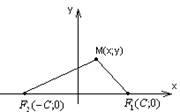
т.М лежит на фокусе, если (есть величина постоянная)

с 0Х:   У=0                

с 0У:   Х=0     =1            

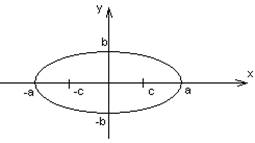
a > b

a называется большей полуосью, a b – меньшей полуосью.

 называется эксцентриситетом.

Для окружности =0, так как у нее больная и малая полуоси равны.

Окружность – частный случай эллипса при .

У окружности оба фокуса совпадают между собой и центром.

Эллипс имеет две оси симметрии т.О(0;0).

Прямые  называются директрисами эллипса.

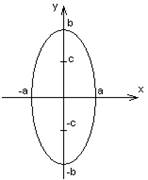
b > a

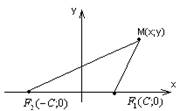
3.  Определение:            Гиперболой называют геометрическое место точек, разность расстояний которое до двух заданных точек, называемых фокусами, есть величина постоянная.

a)       

б) 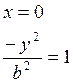       , нет такого у.

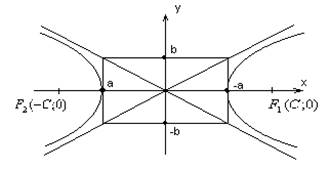
а называется действительной полуосью, а b называется мнимой полуосью.

Гипербола имеет центр симметрии т.0 и ось симметрии, на которой расположены её фокусы.

Симметрия называется её фокальной осью.

Прямые  называется асимптотами симметрии.

 - директриса

a = b, то гипербола называется равнобочной.

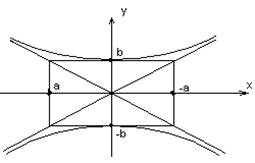
4.  Определение:            Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.

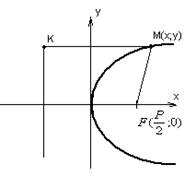
, если

1)       

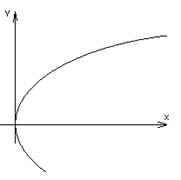
2)       

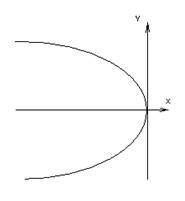
3)       

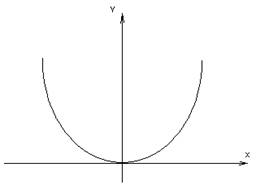
4)       

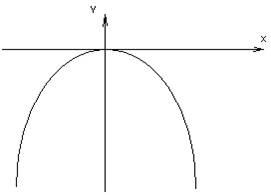
Существует 6 важнейших случаев общего уравнения (1):

1)  Эллипс

2)  Гипербола

3)  Парабола

4)  Пара пересекающихся прямых

5)  Пара параллельных прямых

6)  Точка

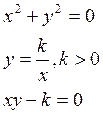
Приведение уравнения кривой второго порядка к каноническому виду:

1.  1)  Параллельный перенос системы координат:

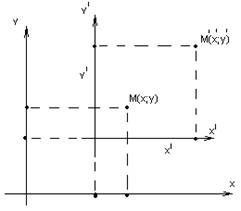
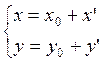
2)  Новые координаты через старые:

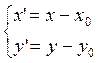
2.         Поворот системы координат на угол

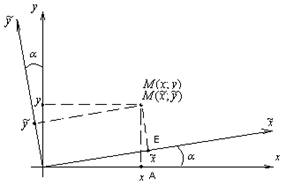
Сначала делают поворот системы координат на такой угол , чтобы исчезло слагаемое, содержащее произведение х и у, при этом sin и cos находят по формуле.

Делают параллельный перенос системы координат в т.О’, выделяя полные квадраты по переменным х и у.

Пример:        

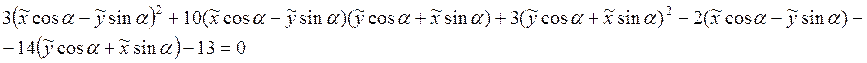
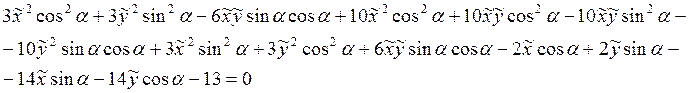
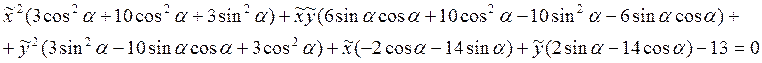
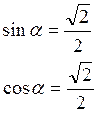
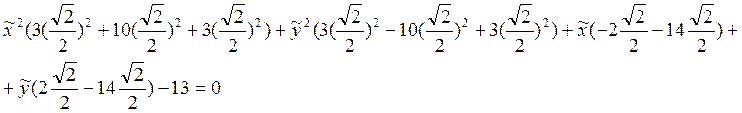
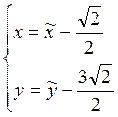
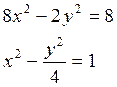
Центр новых координат О’()

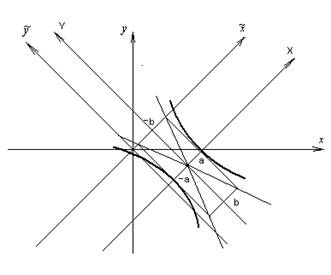
Матрица

Если n=m матрица называется квадратной.

Матрица, все элементы которой равны 0, называется нулевой.

Определение:            Квадратная матрица, у которой все отличные от 0 элементы находятся только на главной диагонали, называется диагональной.

Символ Кроникера  

     

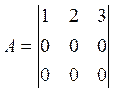
Диагональная матрица, у которой все элементы равны 1, называется единичной.

Любой квадратной матрице ставится в соответствие число, называемое его определителем.

а)        Если определитель равен 0, то матрица называется вырожденной.

б)        Если определитель равен 0, то матрица называется невырожденной.

Определение:            Сумма А+В матриц А и В одинакового размера называется матрица С(i,j), элементы которой считаются по формуле:

    

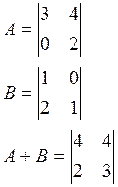
Определение:            Произведением матрицы А на число называют матрицу () , элементы которого считаются по формуле  

Свойства:

1)        А+В=В+А      - коммутативность

2)        А+(С+В)=(А+В)+С   - ассауциативность

3)          - дистрибутивность

4)       

5)        0А=0

6)       

Определение:            Произведением АВ матрицы размером и размером называется размером , где элементы  ищутся по формуле:           

Пример:

1)  Матрицы можно умножать, если число элементов в строке у первой матрицы совпадает с числом элементов в столбце у второго.

2)  Умножение матриц не коммутативно:

Линейная алгебра

Действия над матрицами:

1.  Сложение

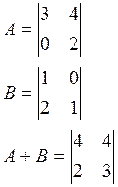
2.  Вычитание

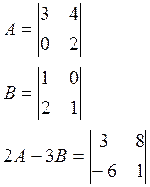
3.  Умножение

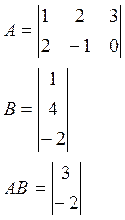
4.         Обратная матрица

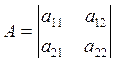
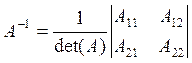
Пример:

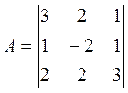
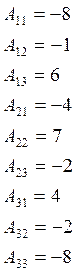
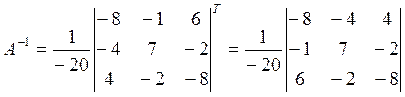
Свойства умножения матриц

1)       

2)       

3)       

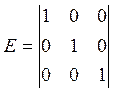
4)       

Свойства транспонирования

1)         

2)       

3)       

4)       

5)       

Если , то матрица называется симметричной.

Пример:

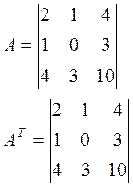
Нахождение обратной матрицы