Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии, страница 13

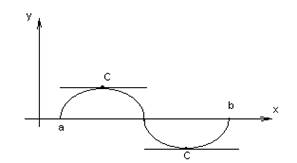
Геометрический смысл:      Если непрерывная кривая, имеющая в каждой точке касательную, пересекает оси 0х в т. (а , 0) и т. (b , 0), то на этой кривой найдется хотя бы одна точка с абсциссой С, (a < С < b), в которой касательная параллельна оси 0х.

Теорема Лагранжа (о конечных приращениях):  Если функция  непрерывна на отрезке  и дифференцируема во всех внутренних точках этого отрезка, то найдется такая т. С (a < С < b), что

Доказательство:      

 - также непрерывна и дифференцируема на отрезке  

, то функция  удовлетворяет условию теоремы Ролля так что

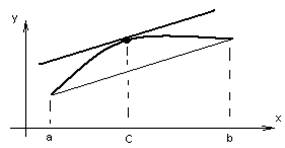
Геометрический смысл:      Величина  - это есть тангенс угла наклона хорды, проходящей через точки  и .

Величина  - это тангенс угла наклона касательной в т. С, таким образом если во всех точках дуги  существует касательная, то на дуге найдется такая точка с абсциссой С, в которой касательная параллельна

Теорема Каши:         Функции  и - две функции непрерывны на отрезке  и дифференцируемы на всех внутренних точках, причем   , то , так что

Доказательство:       , так как если бы то по теореме Ролля что противоречит    - функция  непрерывна на  и дифференцируема на нем, причем  по теореме Ролля  

Раскрытие неопределенностей с помощью производных.

I.

Теорема:        Если функции  и  удовлетворяют условию теоремы Каши и образуются в т. 0, в т. , то если , то .

Пусть , тогда по теореме Каши

    

Пример:        

Замечание:   

1)        Теорема имеет место и в случае, если функции  и не определены при , но       

2)  Если после применения правила Лопиталя неопределенность  осталось и производная удовлетворяет условиям теоремы, то правило применяется еще раз.

3)  Правило Лапиталя применимо также в случае, если .

Доказательство:      

 то

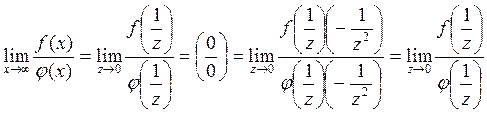
Пример:        

1)       

2)       

3)       

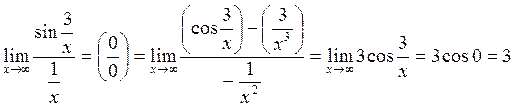
II.        , так что  и может быть равно .

Теорема:        Пусть функции  и  непрерывны и дифференцируемы при всех , в окрестности т. а, причем , тогда если , причем эти пределы при  равны.

Пример:        

Замечание:    Правило Лапиталя справедливо только в том случае, когда предел отношения производных существует.

III.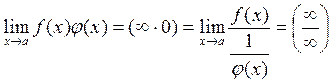      

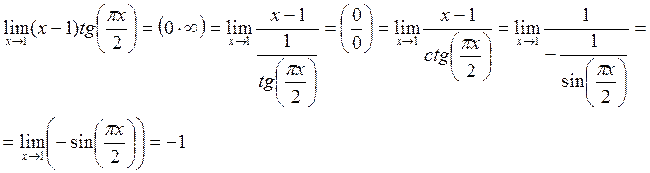
IV.      

В этом случае выражение под знаком предела приводят к общему знаменателю и считают предел.

Пример:

V.       

Пример:

Исследование функций.

Возрастание и убывание функций.

Теорема:       

1)  Если функция , имеющая производную на отрезке , возрастает на этом отрезке, то  при .

2)  Если функция  непрерывна на  и дифференцируема в промежутке  то функция возрастает на .

Доказательство:      

1)        Пусть функция возрастает на .

, так как  - возрастает, то  при  или при , тогда

2)  Пусть , , , тогда по теореме Лагранжа

 при   - это означает, что функция возрастающая.

Теорема:       

1)  Если функция , имеющая производную на отрезке , то убывает на этом промежутке, если ,

2)  Если функция  непрерывна на отрезке  и дифференцируема на нем, причем  при , то функция убывает на отрезке .

Геометрический смысл:     

1)  Если на отрезке  функция возрастает. То касательная к кривой  в каждой точке образует с осью острый угол или в отдельных точках горизонтальна.

2)  Если функция убывает, то угол касательной тупой или в отдельных точках только горизонтальный.

 

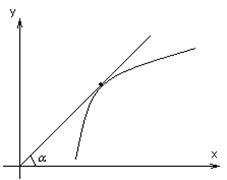
Определение:                       Функция  в т.  имеет максимум, если ее значение в этой точке больше, чем значение во всех точках некоторого интервала т. .

.

Определение:                       Функция  в т.  имеет минимум, если ее значение в этой точке меньше, чем значение во всех точках некоторого интервала т. .

.

Функция  дифференцируема в т.

Определение:                       Точки минимума и максимума называются точками экстремума функции.

Определение:                       Точки, в которых первая производная равна 0 или не существует, называются критическими точками.