2. ![]() - гипербола или пара ее асимптот.
- гипербола или пара ее асимптот.
3. ![]() - парабола.
- парабола.
Пример: Привести кривую к каноническому виду.
![]()
![]()
![]()
![]()
![]() -
эллипс
-
эллипс
1) ![]()
![]()
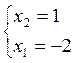
![]()
![]()
2) ![]()
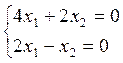
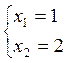
![]()
![]()
![]()
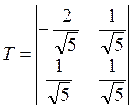
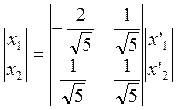
![]()
![]()
![]()
![]()
![]()
![]()
![]() +
+![]()
![]()
Определение: Множеством называется совокупность элементов, объединенных каким-либо признаком.
![]() -
множество В включено во множество А.
-
множество В включено во множество А.
Два множества равны когда ![]() и
и ![]() .
.
Множество, несодержащее элементов
называется множеством ![]() .
.
1) Объединение двух множеств А и В называется множество С, что каждый его элемент принадлежит либо А, либо В, либо А и В.
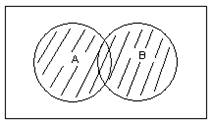
![]()
2)
Пересечение А и В называется множество С, такое что каждый элемент
множества С![]() и А и В.
и А и В.
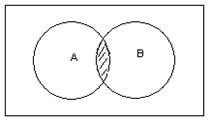
![]()
3) Разностью А и В называется множество С, состоящее из тех элементов множества А, которые не являются элементами множества В.
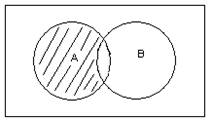
![]()
Определение: Постоянная
величина – это величина, принимающая одно и то же значение (![]() ).
).
Определение: Переменная величина – это величина, принимающая хотя бы два различных значения.
Определение: Совокупностью всех значений, которые принимает величина называется множество ее значений.
Если каждому значению независимой переменной х из какой-то области Д поставить в соответствии определенное значение у. то у называется функцией. Для которой определен у называемый областью определения функции.
Д – множество значений функции.
Е – множество значений функции
Способы задания функции:
1) Графический
2) Аналитический
3) Табличный
Характеристики поведения функции
Основные элементы функции: ![]()
Функция называется не явно
заданной функцией, если задано соотношение ![]()
Если каждому значению х соответствует только одно значение у, то функция называется однозначной.
Если у является функцией от U(y), а U(y) в свою очередь зависит от х, пусть:
![]()
![]()
![]() -
называется функция от функции или сложная функция.
-
называется функция от функции или сложная функция.
Ее область определения является та часть области определения функции U, в которую значения функции не выходят из области определения функции F(U).
Классификация функций.
1. Элементарные функции:
1) Основные элементарные:
![]()
2) Элементарные:
- называется функция, которая
может быть задана первой формулой вида ![]() , где
стоящее справа выражение составлено из основных элементарных функций и
постоянных путем конечного числа операций сложения. Вычитания, умножения,
деления и взятия функции от функции.
, где
стоящее справа выражение составлено из основных элементарных функций и
постоянных путем конечного числа операций сложения. Вычитания, умножения,
деления и взятия функции от функции.
![]()
2. Неэлементарные:
![]()
Обратные тригонометрические функции.
Пусть ![]()
Теорема: У любой однозначной функции есть обратная функция.
Теорема: Для того чтобы
функция ![]() имела однозначную обратную функцию на
интервале (a,b) необходимо и
достаточно, чтобы она была монотонна на данном участке.
имела однозначную обратную функцию на
интервале (a,b) необходимо и
достаточно, чтобы она была монотонна на данном участке.
График обратной симметричной
функции относительно прямой ![]()
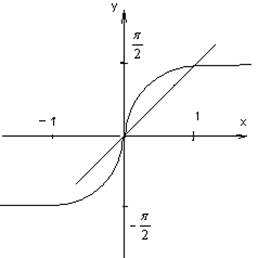
1. ![]()
![]()
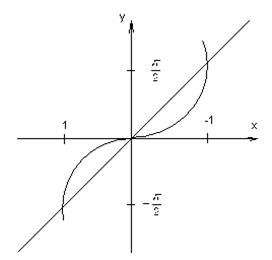
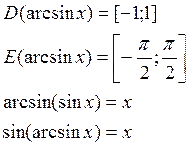
Свойства:
1) Функция нечетная, так как ее график симметричен началу координат.
2) Непериодическая
3) Монотонно возрастающая
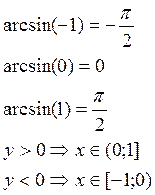
2. ![]()
![]()
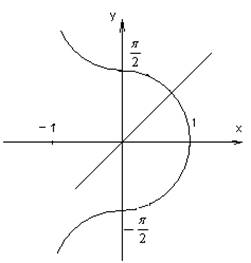
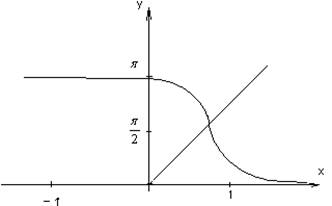
3. ![]()
![]()
4. ![]()
![]()
Функции:
1. Алгебраические
1)
Целая алгебраическая функция (многочлен): ![]()
2)
Дробно-рациональная функция: ![]()
3)
Иррациональная функция: 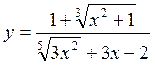
2. Трансцендентные:
Все остальные элементарные функции.
Гиперболические косинус, синус, тангенс, котангенс
1. Гиперболическим
косинусом называется функция: ![]()
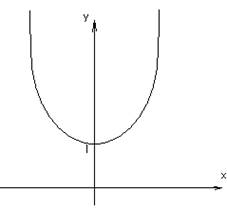
![]()
Свойства:
1) ![]() (вся
действительная прямая)
(вся
действительная прямая)
![]()
2) ![]()
При ![]() функция
убывает
функция
убывает
При ![]() функция
возрастает
функция
возрастает
При ![]()
![]()
![]() при
всех x
при
всех x
2. Гиперболическим
синусом называется функция: ![]()
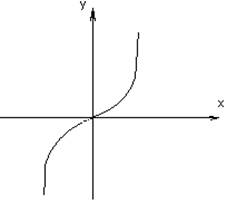
![]()
![]()
![]()
График симметричен относительно начала координат.
Функция возрастает на всей области определения
![]()
![]()
![]()
3. Гиперболический
тангенс: ![]()
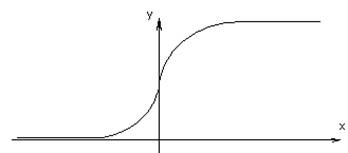
4. Гиперболический
сотангенс: ![]()
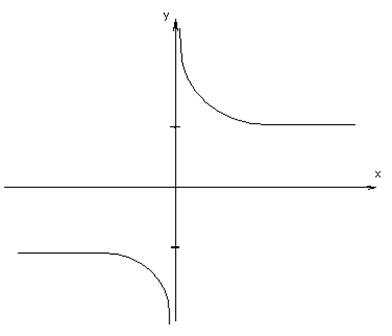
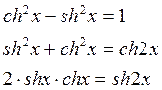
1) ![]()
![]()
![]() -
окружность
-
окружность
2) ![]()
![]()
![]() -
равнобочная гипербола
-
равнобочная гипербола
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.