Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии, страница 10

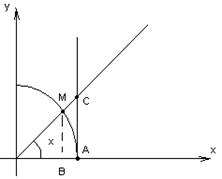
1)       

2)       

3)       

Пример:        

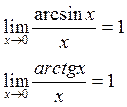
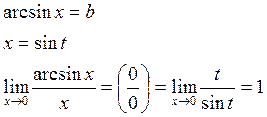
Пример:        

Пример:        

Теорема №9:             Второй замечательный предел.

Доказательство:      

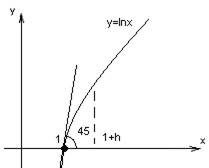
Пример:        

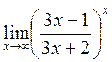
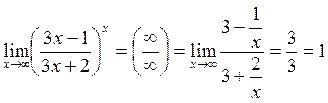
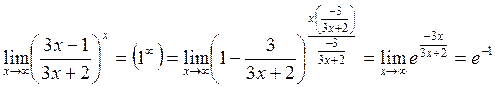
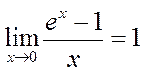
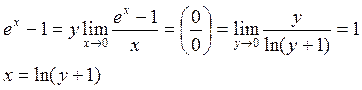
Сравнение бесконечно малых величин

Пусть БМВ  и  стремятся к 0 при.

Определение:                       Если отношение  имеет конечный и отличный от 0 предел , то и  называются БМВ одного порядка.

Пример:          и

При вычислении пределов БМВ можно менять на эквивалентную.

Теорема:        Если , а , то

Пример:        

0, то БМВ называется БМВ высшего порядка, а - низшего порядка.

Определение:                       Если , то БМВназывается БМВ k-того порядка, относительно БМВ .

 при k = 2.

БМВ и  эквивалентны тогда и только тогда, когда их разность есть БМВ высшего порядка, чем и .

Непрерывность функций.

Определение:                       Пусть  определена в т.  и в некоторой окрестности , если переменная  получает приращение .

Приращением функции у называется величина

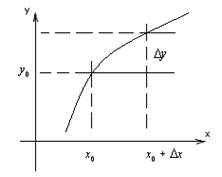
Определение:                       Функция  называется непрерывной в т. , если она определена в некоторой окрестности т.  и     

, то есть предел непрерывной функции в т.  равен значению функции в этой точке.

Пример:        

Теорема:        Все основные элементарные функции непрерывны всюду. Где они определены.

Пример:        

Правило:        Для непрерывной функции знак предела и знак функции можно менять местами.

Пусть и  непрерывны в т. , тогда

1)        , каждая непрерывна  в т.

2)         непрерывна в т.

3)         непрерывна в т.

4)         непрерывна  в т.  и равна , то - непрерывна в т. .

Доказательство:       Пусть  и , то

Теорема:                    Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Доказательство теоремы следует из определения элементарной функции и предыдущей теоремы.

Определение:                       Если функция  непрерывна в каждой точке некоторого интервала , то она называется непрерывной на этом интервале.

Определение:                      

1)        Если в какой –либо точке функция  не определена или  или , то при  функция разрывна, т.  называется точкой разрыва функции.

2)        Если функция  такая, что существует конечные пределы и , но или они не равны или не совпадают со значением функции в т. , то т.  называется точкой разрыва  первого рода.

 называется скачком функции в значении в т. .

3)        Если для функции какой-то из пределом  или  не существует или не равен , то т.  называется устранимой точкой разрыва функции.

4)        Если же , то в т.  функция не определена и т.  называется устранимой точкой разрыва функции.

Пример:        

1)       

- точка разрыва.

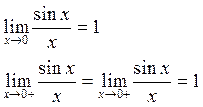
-устранимая точка разрыва.

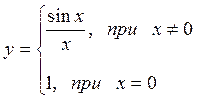
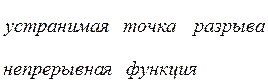
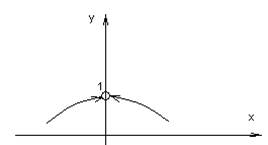
2)       

 имеет разрыв первого рода скачок в нуле = 2

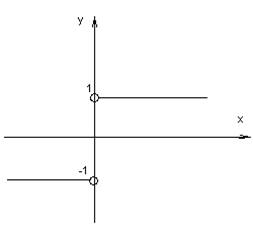
3)       

= 1 – т. разрыва

Некоторые свойства непрерывной функции

Теорема:                    Если функция  непрерывна на отрезке, то на отрезке найдется хотя бы одна т. такая, что для всех точек отрезка  выполнено соотношение  и найдется хотя бы одна т.  такая, что .

Определение:                       Значение  называется наибольшим значением функции на отрезке , а - наименьшим.

Теорема №1:             Непрерывная на отрезке  функция достигает наибольшего значения М и наименьшего значения m.

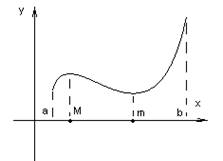
Отрезок нельзя заменять интервалом, так как теорема может оказаться неверной.

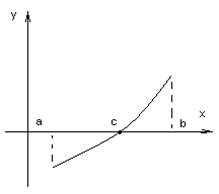
Теорема №2:             Пусть функция  непрерывна на отрезке и на концах отрезка принимает значения разных знаков, тогда между т. а  и т. b найдется, по крайней мере, одна т. с на которой функция обращается в 0.

Функция  соединяет точки  и , причем  пересекает ось хотя бы в одной точке.

Теорема №3:             Пусть функция  определена и непрерывна на отрезке [a,b], если на концах этого отрезка функция принимает неравные значения, то для любого числа М. заключенного между чисел a и b найдется такая т. с, принадлежащая отрезку, что .