![]()
![]()
![]()

Всякая прямая ![]() , где
, где ![]() ,
пересекает график функции
,
пересекает график функции ![]() .
.
Теорема №2 является следствием
теоремы №3 при ![]() .
.
Следствие: Если ![]() непрерывна на некотором интервале и
принимает наибольшие и наименьшие значения, то на этом интервале она принимает
хотя бы один раз любое значение, заключенное между наибольшим и наименьшим
значениями.
непрерывна на некотором интервале и
принимает наибольшие и наименьшие значения, то на этом интервале она принимает
хотя бы один раз любое значение, заключенное между наибольшим и наименьшим
значениями.
Производная.
Пусть функция ![]() определена на некотором промежутке.
определена на некотором промежутке.
Производной называется предел
отношения приращения функции ![]() к приращению
к приращению ![]() , когда
, когда ![]() .
.
![]()
![]()
Производная функции зависит от элементов.
Операция нахождения производной от функции называется дифференцирование.
![]()
Физический смыслы производной:
Рассмотрим прямолинейное движение
т. ![]() , отсчитываемое от начального момента т.
, отсчитываемое от начального момента т.
![]() .
.
![]()
Пусть во время ![]() точка находится в т.
точка находится в т. ![]() , а во время
, а во время ![]() в
положении т.
в
положении т. ![]() . Путь равен
. Путь равен ![]() . За
время
. За
время ![]() путь получил приращение
путь получил приращение ![]() . Отношение
. Отношение ![]() называется
средней скоростью движения за время
называется
средней скоростью движения за время ![]() . Предел средней
скорости называется скоростью движения точки в данный момент.
. Предел средней
скорости называется скоростью движения точки в данный момент.
![]()
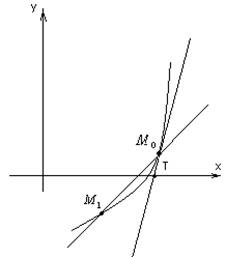
Геометрический смысл производной:
![]()
Определение: Если
при неограниченном приближении т. ![]() по кривой
по кривой ![]() в т.
в т. ![]() с
любой стороны секущая стремиться занять положение, определенное прямой
с
любой стороны секущая стремиться занять положение, определенное прямой ![]() , называемой касательной к кривой в т.
, называемой касательной к кривой в т. ![]() .
.
![]()
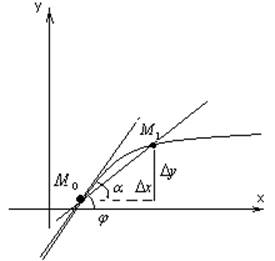
![]() -
угол образования секущей, движущейся в направлении линии
-
угол образования секущей, движущейся в направлении линии ![]()
![]()
![]()
Прямая, проходящая через т. ![]() и составляет
и составляет ![]() ,
будет искомой касательной.
,
будет искомой касательной.
![]()
Производная в каждой точке равна
угловому коэффициенту касательной к графику в этой точке. Прямая, проходящая
через т. ![]() перпендикулярна касательной в этой
точке называется нормалью.
перпендикулярна касательной в этой
точке называется нормалью.
![]() -
уравнение касательной.
-
уравнение касательной.
![]() -
уравнение нормали.
-
уравнение нормали.
Пример: Составить уравнение
касательной и нормали кривой ![]() в т.
в т. ![]() =1.
=1.
![]()
![]()
![]()
![]() -
уравнение касательной.
-
уравнение касательной.
![]() -
уравнение нормали.
-
уравнение нормали.
Дифференцируемость функции.
Определение: Если
функция ![]() имеет производную в т.
имеет производную в т. ![]() , то она называется дифференцируемой в
т.
, то она называется дифференцируемой в
т. ![]() .
.
Определение: Если
функция ![]() имеет производную в каждой точке
интервала, то она называется дифференцируемой на интервале.
имеет производную в каждой точке
интервала, то она называется дифференцируемой на интервале.
Теорема: Если функция
![]() дифференцируема в некоторой т.
дифференцируема в некоторой т. ![]() , то она в этой точке непрерывна.
, то она в этой точке непрерывна.
Доказательство: ![]() по теореме о пределах
по теореме о пределах ![]()
![]()
![]() функция
непрерывна.
функция
непрерывна.
Замечания:
1) В точке разрыва у функции нет производной.
2) Обратное утверждение неверно – из непрерывности функции не следует ее дифференцируемость.
Пример: ![]()
При ![]() функция
непрерывна, но не дифференцируема.
функция
непрерывна, но не дифференцируема.
![]() ,
тогда
,
тогда ![]()
Пусть ![]()
![]()
Дифференцируемость ![]() непрерывность.
непрерывность.
Непрерывность![]() недифференцируемость.
недифференцируемость.
Непрерывность![]() дифференцируемость.
дифференцируемость.
Схема нахождения производной.
1) Даем аргументу
приращение ![]() и вычисляем
и вычисляем ![]() .
.
2) Находим ![]()
3) Составляем
отношение ![]()
4) Считаем ![]()
Формулы с производной:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
Теорема: Производная
логарифмической функции ![]() (формула №11).
(формула №11).
Доказательство: ![]()
![]()
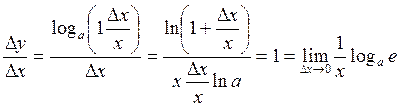
![]() (формула
№12).
(формула
№12).
Теорема: Производная показательной
функции ![]() (формула №13).
(формула №13).
Доказательство: ![]()
![]()
![]()
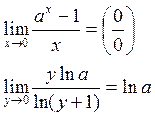
![]()
![]()
![]()
![]()
Следствия: Производная от
сложной функции ![]()
![]() , где
, где
![]() ,
, ![]() называется
внешней функцией,
называется
внешней функцией, ![]() - промежуточной.
- промежуточной.
Теорема: а) Если функции ![]() имеет в некоторой т. х производную
имеет в некоторой т. х производную ![]() . А функция
. А функция ![]() имеет
при соответствующих значениях
имеет
при соответствующих значениях ![]() производную
производную ![]()
![]() (формула
№14).
(формула
№14).
б) Производная сложной функции равна произведению производной внешней функции по промежуточному аргументу на произведение промежуточного аргумента по х.
Доказательство: Приращение ![]() соответствует приращению
соответствует приращению ![]() , который соответствует приращению
, который соответствует приращению ![]() :
: ![]()
![]()
![]()
![]()
![]()
Пример: ![]()
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
![]()
Производные гиперболических функций:
1) 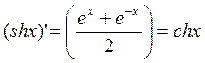 (формула
№15)
(формула
№15)
2) 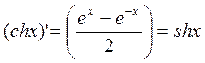 (формула
№16)
(формула
№16)
3) ![]() (формула
№17)
(формула
№17)
4) ![]() (формула
№18)
(формула
№18)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.