Определители. Формула Крамера решения системы линейных алгебраических уравнений. Элементы векторной алгебры и аналитической геометрии, страница 9

Определение:                        называется множество точек оси, удовлетворяющей неравенство. (-окрестность)

Определение:                       Окрестностьюбесконечно-удаленной точки называется множество точек оси, удовлетворяющей условие: , где М>0.

Определение:                       Пусть функция  определена в некоторой окрестности т. а, тогда  при , если   () 

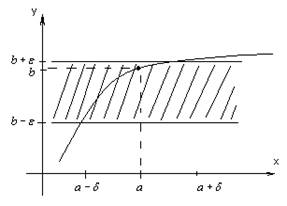
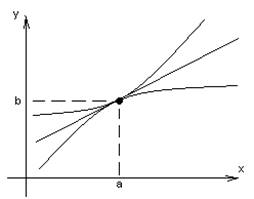
Для любых x, отстоящих от а не более чем на , точки графика  лежат внутри полосы шириной , ограниченной прямыми  и .

Если  при  так, что х принимает значения меньше а, то пишут  и число  называется пределом функции  при .

Если х принимает значение больше а, то пишут  и число  называется пределом  при  , то и будет пределом функции.

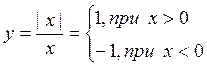
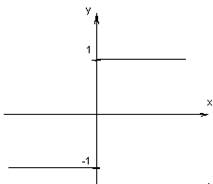
Пример:         Показать по определению предела, что

при      

Определение:                        при, если     такое, что .

Пример:        

Определение:                      

Определение:                       Функция f(x)  называется бесконечно большой величиной при , если

Определение:                        при , если

Определение:                       Функция f(x) называется ограниченной на интервале , если . Если М не существует, то функция называется неограниченной на интервале из обычных  и , так как  и .

Определение:                       Функция f(x) называется ограниченной при , если  с центром в т. А. в котором данная функция ограничена.

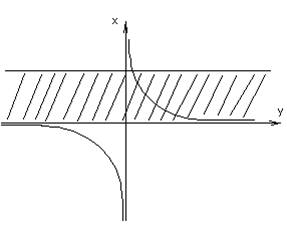
Функция

В окрестности т.1 – ограниченна

В окрестности т.0 – неограниченна.

Определение:                       Функция f(x) называется ограниченной при , если - ограниченная функция.

Определение:                       Функция натурального аргумента называется последовательностью ()

Определение:                       Число b называется пределом последовательности y(n), если

Пример:         . Пусть , то

Свойства бесконечно большой величины (ббв):

1)  сумма ббв есть величина бесконечно большая;

2)  Произведение ббв на ограниченную есть величина бесконечно большая;

3)  Произведение ббв есть величина бесконечно большая;

Неопределенности:

1)        ;

2)        ;

3)        .

Определение:                       Функция называется бесконечно малой величиной (бмв) при , если  .

Свойства бмв:

1)  Величина, обратная ббв, есть бмв;

2)  Сумма бмв есть бмв;

3)  Произведение бмв есть бмв;

4)  Сумма бмв на ограниченную есть бмв

Неопределенности:

1)       

2)       

Основные теоремы о пределах.

Теорема №1:             Если  представима в виде суммы постоянного числа b и  БМВ при , то

Если , то , где БМВ при .

Доказательство:      

1)        , тогда

2)       

Теорема №2:             а)         Если   , то найдется такая т.А, для любых точек которой

Доказательство:       такое, что

, тогда   

Следствие:    Если  и , то все значения переменной у, начиная с некоторого, также будут .

Теорема №3:             Функция  при  не может одновременно стремиться двум разным пределам.

Доказательство:      

 и    при

, тогда по теореме №2    и  

Пусть , тогда при этом N должны выполняться оба неравенства, что не возможно.

Теорема №4:             Пусть  и , тогда:

1)        (на основании теоремы №1: , где БМВ при и  , где БМВ при .

2)       

3)           при

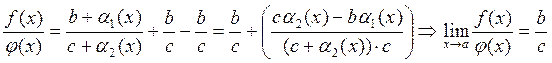
Теорема №5:             Если для соответствующих значений двух функций  и , стремящихся к пределам , выполняется неравенство , то    , тогда по теореме №2

Теорема №6:             Если , то  является ограниченной функцией при  .

Доказательство:           

.

Теорема №7:             Если для соответствующий значений трех функций выполняется неравенство  и при этом , то при  

.

Доказательство:        

и найдется другая т.а. в которой . Возьмем меньшую из двух , тогда будут выполняться оба неравенства

Теорема №8:             Первый замечательный предел.

Доказательство: