Система ДУ.
Нормальная система ОДУ порядка n называется совокупность диффиринциальных уравнений первого порядка вида:
(1) 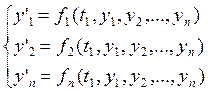
где функции ![]() определены и
непрерывные на множестве
определены и
непрерывные на множестве ![]() ,
, ![]() - независимая переменная,
- независимая переменная, ![]() - искомые функции,
- искомые функции, ![]() - их производные.
- их производные.
Кратный вид: ![]()
Введём вектор ![]()
![]()
и вектор ![]()
![]()
![]()
В нормальной системе все уравнения разрешимы относительно производных и имеют 1 порядок.
Решением на интервале ![]() нормальной
системы ОДУ называется совокупность n диффиринцируемых
на I функций
нормальной
системы ОДУ называется совокупность n диффиринцируемых
на I функций ![]() , такая что точка принадлежит
, такая что точка принадлежит ![]() и имеет место равенство
и имеет место равенство ![]() Решением в неявном виде системы (1) на
интервале
Решением в неявном виде системы (1) на
интервале ![]() называется совокупность n соотношений
называется совокупность n соотношений ![]() ,
i=1,2,…,n определяющих совокупность
неявных функций
,
i=1,2,…,n определяющих совокупность
неявных функций ![]() которые являются решение
системы (1) на интервале функции.
которые являются решение
системы (1) на интервале функции.
Задача Каши.
Задача Каши для системы (1) формулируется следующим образом:
найти решение системы (1) удовлетворяющие условиям ![]() (2),
где
(2),
где ![]() -заданные числа.
-заданные числа.
Теорема: Пусть правая часть fi нормальная система (1) и их частные производные по
переменным y1,y2,…,yn определены и непрерывны
на множестве ![]() , тогда в некоторой окрестности в точке t0 существует непрерывное решение задачи каши (1),
(2) и оно единственно.
, тогда в некоторой окрестности в точке t0 существует непрерывное решение задачи каши (1),
(2) и оно единственно.
![]()
множество Д в каждой точке которого существует единственное решение задачи Каши называется областью единственности системы (1).
Пусть Д область единственности системы (1) совокупность n функций ![]() i=1,2,…,n (3)зависящих от n параметров
С1,С2,…,Сn и имеющих
непрерывные частные производные по t называются
общим решением системы (1) если:
i=1,2,…,n (3)зависящих от n параметров
С1,С2,…,Сn и имеющих
непрерывные частные производные по t называются
общим решением системы (1) если:
Общим решением в неявном виде или общим интегралом системы (1) называется совокупность n соотношений содержащие n параметров С1,С2,..,Сn и в неявном виде описывающие семейство функций являющееся общим решением системы (1) в Д.
Решением системы (1) во всех точках которого выполняется свойства единственности решения задачи Каши называется частным решением системы (1). Решение системы (1) во всех точках которого нарушено свойство единственности называется особым решением системы (1). Решение системы (1) не являющееся частным или особым называется составным решением. Замечание: все решения полученные из общего при конкретных значениях констант Сi является частным решением.
Метод исключений.
(1) 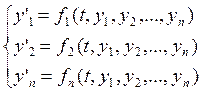
Продифференцируем первое уравнение системы по переменной t:
![]()
![]()
![]()
![]()
![]()
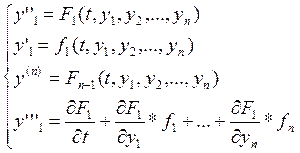
Из первых n-1 уравнений системы находят выражения: y2,y3,…,yn через t,y1,y'1,…,y(n-1)1 и подставляют в первое уравнение системы. Тогда последнее уравнение получается ЛНДУ n порядка относительно y1.
Нормальные системы ЛОДУ с постоянными коэффициентами.
![]()
(5) 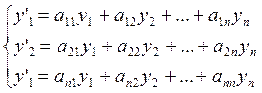
aij –искомые функции
A=(aij)
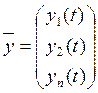
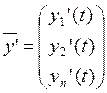
Запись (5) в векторной форме имеет вид ![]() =A
=A![]()
Вектор функции ![]() называется линейно-зависимым
если существует константы
называется линейно-зависимым
если существует константы ![]() не равные 0
одновременно, такие что их линейная комбинация равна 0. Совокупность n линейно-зависимых решений (5)
называется фундаментальной системой решений.
не равные 0
одновременно, такие что их линейная комбинация равна 0. Совокупность n линейно-зависимых решений (5)
называется фундаментальной системой решений.
Теорема: если совокупность вектора функции является фундаментальной
системой решений, то общее решение системы записывается в виде:![]()
Решение системы в случае простых корней характеристического уравнения. Метод Эйлера.
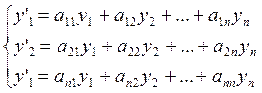
![]()
![]()
![]()
![]()
![]()
![]()
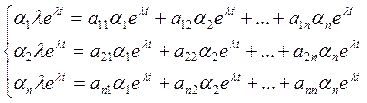
Сокращаем на ![]()
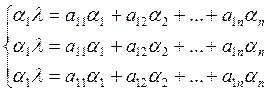
и приводим подобные однородная система: 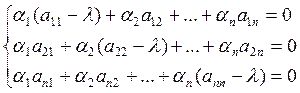
![]() ,
,![]() ,…,
,…,![]() - неизвестные
- неизвестные
Однородная система имеет не тривиальное решение когда её
определитель равен 0 ![]()
![]() собственное
значение матрицы А
собственное
значение матрицы А
![]() координаты собственного
вектора.
координаты собственного
вектора.
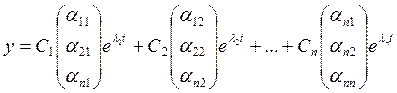
Решение задачи Каши матричным способом.
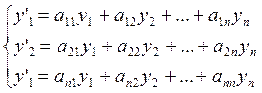
y1(t0)=y10
y2(t0)=y20
yn(t0)=yn0
![]()
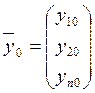
Пусть фундаментальная система решений ![]() найдено. Матрицу Y(t) составленную из компонентов этих решений называют
фундаментальной матрицей.
найдено. Матрицу Y(t) составленную из компонентов этих решений называют
фундаментальной матрицей.
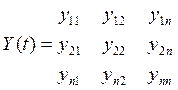
Y(t) удовлетворяет матричному уравнению Y'=AY
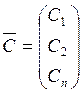 , тогда общее решение
, тогда общее решение![]()
![]() есть
есть ![]()
y(t0)=Y(t0)![]()
![]()
![]()
![]()
Неоднородные нормальные системы структура общего решения.
Нормальная система вида:
(1) 
где fi – непрерывные функции называемые неоднородными.
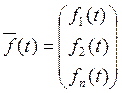
![]()
Теорема 1: если ![]() решение неоднородной
системы, а
решение неоднородной
системы, а ![]() решение соответствующей однородной
системы, то
решение соответствующей однородной
системы, то![]() так же есть решение неоднородной
системы.
так же есть решение неоднородной
системы.
Доказательство.
![]()
![]()
![]()
![]()
![]()
![]()
что верно так как ![]() решение неоднородной
системы.
решение неоднородной
системы.
Теорема 2: общее решение ![]() неоднородной
системы есть сумма общего решения однородной системы и частного решения
неоднородной системы
неоднородной
системы есть сумма общего решения однородной системы и частного решения
неоднородной системы ![]() (2).
(2).
Доказательство.
Из теоремы 1 следует что (2) дает решение неоднородной системы. Покажем что функция (2) позволяет решить задачу Каши по начальным условиям.
![]()
![]()
где функции ![]() ,
,![]() ,…,
,…,![]() образуют
фундаментальную систему решений, С1,С2,…,Сn - произвольные постоянные.
образуют
фундаментальную систему решений, С1,С2,…,Сn - произвольные постоянные.
![]()
![]()
![]()
подставим
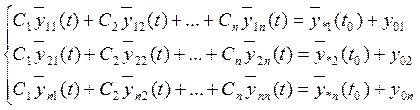
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.