Циркуляцией векторного поля вдоль замкнутого контура равна
потоку вихря поля через поверхность натянутую на этот контур. Из формулы стокса
следует равносильное определение ![]() .
.
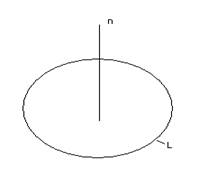
Пусть ![]() плоская площадка,
содержащая данную точку перпендикулярно направлению n и L контур
ограничивающий эту площадку.
плоская площадка,
содержащая данную точку перпендикулярно направлению n и L контур
ограничивающий эту площадку.
Тогда ![]() поля в точке
определяется равенством:
поля в точке
определяется равенством: 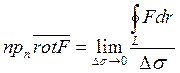 проекция
проекция ![]() на каждое направление равна приделу
отношения циркуляции вдоль линии L площади
на каждое направление равна приделу
отношения циркуляции вдоль линии L площади
![]() когда площадка
когда площадка ![]() стягивается
в точку.
стягивается
в точку.
Оператор Гамильтона. Потенциальное и соленоидальное поле. Операции второго порядка.
Введем символьный вектор набла ![]()
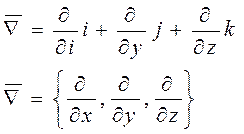
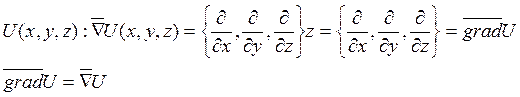
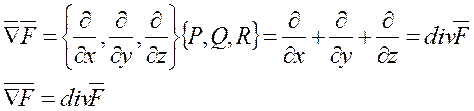
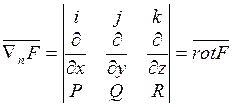
Вектор ![]() называется
оператором Гамильтона. Пусть поле
называется
оператором Гамильтона. Пусть поле ![]() потенциально, т.е.
существует функция U=U(x,y,z) называется
его потенциалом, такая что
потенциально, т.е.
существует функция U=U(x,y,z) называется
его потенциалом, такая что
![]() т.е.
т.е.
![]()
Посчитаем ротор этого поля:
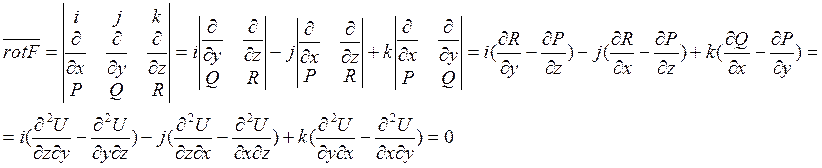
![]() поле потенциально.
поле потенциально.
Векторное поле, для которого ![]() называется безвихривым. Условие
потенциальности поля является равенство 0 его ротора (
называется безвихривым. Условие
потенциальности поля является равенство 0 его ротора ( ![]() ).
).
![]() условие потенциальности для двумерного
случая.
условие потенциальности для двумерного
случая.
Докажем что эти условия эквивалентны.
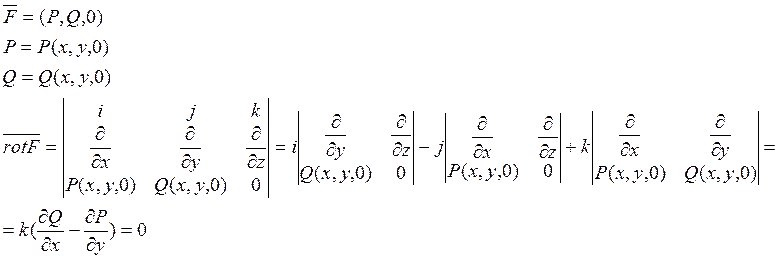
![]() условие равенства
условие равенства ![]() для двумерного случая.
для двумерного случая.
Векторное поле ![]() для которого
для которого ![]() называется
соленоидальным или трубчатым. Пусть
называется
соленоидальным или трубчатым. Пусть ![]() любая кусочногладкая
поверхность.
любая кусочногладкая
поверхность.

![]() ,
тогда
,
тогда ![]()
Пусть теперь поле соленоидально ![]()
![]() . Значит
. Значит
![]() . Выберем вектор
. Выберем вектор ![]()
![]() касательным к поверхности
касательным к поверхности ![]() в любой точке.
в любой точке.
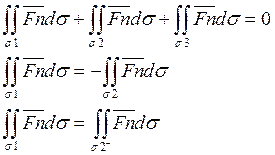
Для соленоидального поля
количество жидкости втекающей в трубку равно количеству вытекающей жидкости и
поток через различные сечения одинаков. Пусть ![]() какое
либо поле, тогда его вихри образуют векторное поле
какое
либо поле, тогда его вихри образуют векторное поле ![]() .
Посчитаем
.
Посчитаем ![]()
![]() - это
смешанное произведение трех векторов два из которых равны. Такое смешанное
произведение равно 0 по определению, т.е. поле
- это
смешанное произведение трех векторов два из которых равны. Такое смешанное
произведение равно 0 по определению, т.е. поле ![]() является
соленоидальным полем.
является
соленоидальным полем.
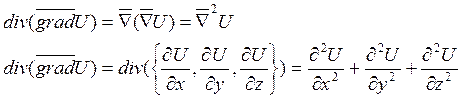
Оператор Лапласа: ![]()
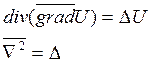
Теория функции комплексной переменной.
z=a+jb – алгебраическая
z=![]() - тригонометрическая
- тригонометрическая
![]() - показательная
- показательная
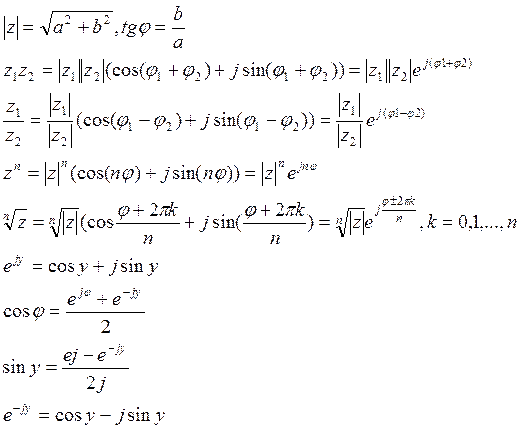
Заменим действительное число y комплексным числом z:
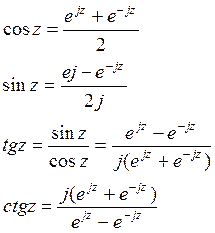
Говорят что на множестве точек
изображающих значения комплексных переменных z определена функция, ![]() если
в каждой точке z этого
множества поставлено соответствие: одно в случае однозначной функции, или
несколько в случае многозначной функции – W, т.е.
задание комплексной функции равносильно заданию двум зависимым U=U(x,y),
если
в каждой точке z этого
множества поставлено соответствие: одно в случае однозначной функции, или
несколько в случае многозначной функции – W, т.е.
задание комплексной функции равносильно заданию двум зависимым U=U(x,y), ![]()
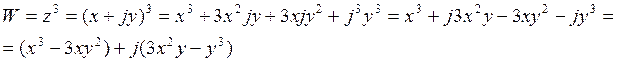
Основные элементарные функции комплексных переменных.
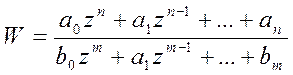 -
однозначная определена при всех z не
являющимися корнями в знаменателе.
-
однозначная определена при всех z не
являющимися корнями в знаменателе.
![]() -
рациональная функция.
-
рациональная функция.
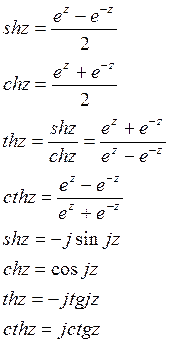
Если ![]() то W называется логарифмом числа z
то W называется логарифмом числа z ![]()
Пусть ![]()
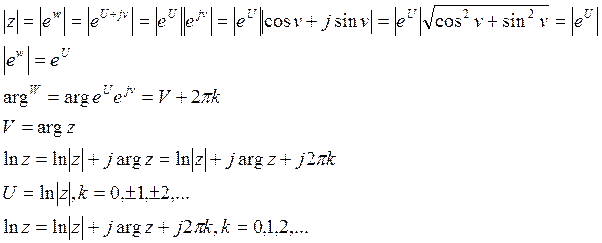
Из-за многозначности argz логарифм является многозначной функцией. Lnz называется значением соответствующие k=0.
Пусть z=x действительное число, ![]() в этом случае главное значение совпадает
со значением обычной функции y=lnx.
в этом случае главное значение совпадает
со значением обычной функции y=lnx.
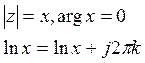
k=0- главное значение получается при k=0, Lnx=lnx.
Если z=sinW, то W называют arcsin числа z и обозначают W=arcsinz.
![]()
Пусть z действительное число, такое что ![]() -
действительное число и
-
действительное число и ![]() , тогда все значения
логарифма чисто мнимые, а все значения arcsinz – действительные.
, тогда все значения
логарифма чисто мнимые, а все значения arcsinz – действительные.
![]()
Если z=cosW, то W называется arccosz и обозначает z=cosW.
W=arccosz.
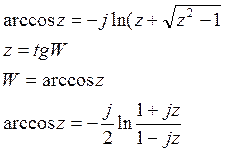
Предел и непрерывность функции комплексной переменной.
Число ![]() называется
пределом f(z).
называется
пределом f(z). ![]() если для любой
если для любой ![]()
![]() -окрестности в точке
-окрестности в точке ![]() можно найти
можно найти ![]() -окрестность
в точке
-окрестность
в точке ![]() , что для всех точек этой окрестности
кроме
, что для всех точек этой окрестности
кроме ![]() соответствующие значения функции f(z) будут принадлежать
соответствующие значения функции f(z) будут принадлежать ![]() -окрестности в точке
-окрестности в точке ![]() .
.
Если функция W=f(z) определена в ![]() и в некоторой её окрестности и
и в некоторой её окрестности и ![]() существует и равен
существует и равен ![]() , то f(z) называется непрерывной в
, то f(z) называется непрерывной в ![]() .
.
Производная от функции комплексного переменного.
Пусть задана функция W=f(z). Дадим
z=x+jy приращение ![]() , тогда W получит приращение
, тогда W получит приращение ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.