получена неопределенная система имеет единственное решение
когда её определитель отличается от 0 что выполняется так как ![]() , а он не равен 0
, а он не равен 0![]() каковы
бы небыли начальные условия существует набор констант С1*,С2*,…,Сn*такие что начальные условия выполняются,
т.е. (2) дает большое решение.
каковы
бы небыли начальные условия существует набор констант С1*,С2*,…,Сn*такие что начальные условия выполняются,
т.е. (2) дает большое решение.
Для нахождения частного решения y* применяют метод Лагранжа вариации произвольных постоянных:
![]() , тогда частное решение ищем в
виде
, тогда частное решение ищем в
виде
![]()
![]() это есть система уравнений
относительно С'1(t),C'2(t),…,C'n(t) относительно этой системы есть определитель
фундаментальной матрицы который не равен 0
это есть система уравнений
относительно С'1(t),C'2(t),…,C'n(t) относительно этой системы есть определитель
фундаментальной матрицы который не равен 0![]() существует
решение С'1(t),C'2(t),…,C'n(t).
существует
решение С'1(t),C'2(t),…,C'n(t).
Понятие об устойчивости.
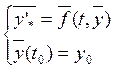
![]()
Решением системы называют устойчивым по Лепунову в
положительном направлении если оно непрерывно по t0
в интервале ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Геометрическая устойчивость означает, что все решения
близкие в начальный момент к решению y(t) не выходят за пределы E трубки при всех ![]()
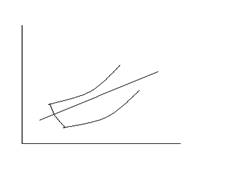
Если отклонение стремится к 0 при достаточно малых ![]() то решение называется агентатически
устойчивым
то решение называется агентатически
устойчивым ![]()
![]()
Любое решение начинается в начальный момент в ![]() трубке неограниченно с течением времени
приближается к y(t). Трубка
радиуса
трубке неограниченно с течением времени
приближается к y(t). Трубка
радиуса ![]() называется областью притяжения решений.
называется областью притяжения решений.
Кратные интегралы. Двойные интегралы.
Пусть на плоскости XOY задана
область Д ограниченная линией L и функцией z=f(x,y) непрерывна в Д. Разобьем область Д линиями на n частей, часть ![]() в каждой из площадок
в каждой из площадок ![]() возьмём точку
возьмём точку ![]() посчитаем
в каждой точке
посчитаем
в каждой точке ![]() значение функции
значение функции ![]() и составим сумму:
и составим сумму: ![]() это интегральная сумма для f(x,y) в
области Д. Если f(x,y)
это интегральная сумма для f(x,y) в
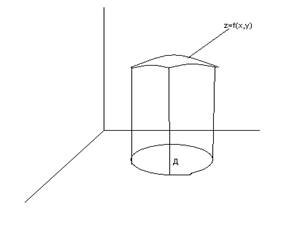
области Д. Если f(x,y)![]() в Д, то выражение
в Д, то выражение ![]() есть объем цилиндра с основанием
есть объем цилиндра с основанием ![]() и высотой
и высотой ![]() . Vn есть сумма
объемов элементарных цилиндров равная объему ступенчатого тела.
. Vn есть сумма
объемов элементарных цилиндров равная объему ступенчатого тела.
Рассмотрим произвольную последовательность интегральных сумм
![]() ,
,![]() ,
,![]() … при различных способах разбиения
области Д, и пусть максимальный диаметр площадок стремится к 0 при
… при различных способах разбиения
области Д, и пусть максимальный диаметр площадок стремится к 0 при ![]() .
.
Если существует придел последовательности интегральных сумм ![]() и этот предел не зависит ни от способа
разбиения тел на площадке, ни от
и этот предел не зависит ни от способа
разбиения тел на площадке, ни от ![]() , то он называется двойным
интегралом от функции f(x,y) по области Д.
, то он называется двойным
интегралом от функции f(x,y) по области Д.
Если f(x,y)![]() 0 в Д, то
двойной интеграл есть объем тела ограниченного поверхностью z=f(x,y) плоскостью
z=0 и цилиндрической поверхностью образующие которой
параллельны оси OZ, а направляющей служит граница
области Д.
0 в Д, то
двойной интеграл есть объем тела ограниченного поверхностью z=f(x,y) плоскостью
z=0 и цилиндрической поверхностью образующие которой
параллельны оси OZ, а направляющей служит граница
области Д.
Теорема 1: Двойной интеграл от суммы двух функций ![]() равен сумме двойных интегралов от каждой
функции отдельно.
равен сумме двойных интегралов от каждой
функции отдельно.
Доказательство.
По определению 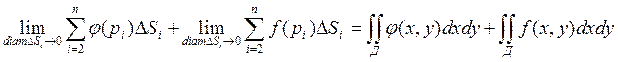
По определению предела 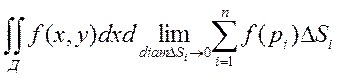
Теорема 2: Постоянный множитель можно выносить за знак
двойного интеграла ![]()
Теорема 3: Если область Д разбить да 2 области без общих
внутренних точек и функция f(x,y) непрерывна во всех точках области Д, то ![]()
Доказательство.
Т.К. при построении интегральной суммы разбиение области на
площади произвольно, то разбивают так чтобы общая граница Д1Д2 являлась
границей соответственных площадок. ![]() переходя к пределу
при
переходя к пределу
при ![]() получаем доказываемое равенство.
получаем доказываемое равенство.
Двукратный интеграл.
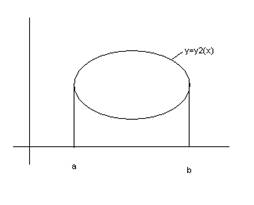
Пусть область Д обладает свойствами. Всякая прямая параллельная оси OY и проходящая через внутреннюю точку области пересекает её границу в двух точках. Такая область называется правильной в направлении оси OY.
Область Д называется правильной в направлении оси OX если всякая прямая проходящая через внутреннюю точку области параллельной оси OX пересекает её границу в двух точках.
Область правильная в обеих направлениях называется просто правильная область.
![]()
![]()
Повторным или двукратным интегралом называется следующий
интеграл: 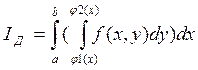
При вычислении сначала считается внутренний интеграл по переменной y, x принимается const, потом интегрируется по x.
Свойства:
1) Если
правильная в направлении оси OY или
OX Д разбить на две области Д1 и Д2 прямой параллельной
OY или OX,
то двукратный интеграл по Д будет равен сумме интегралов: ![]()
Следствие: Если одни из функций ![]() и
и ![]() не может быть задана параметрически
одним выражением на отрезке АВ, т.е. существует
не может быть задана параметрически
одним выражением на отрезке АВ, т.е. существует ![]() такая
что
такая
что ![]() , то
, то 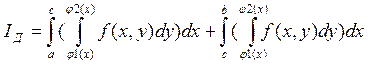
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.