Система дифференциальных уравнений. Задача Каши. Нормальные системы ЛОДУ с постоянными коэффициентами, страница 3

2)  Пусть m и М наименьшее и наибольшее значения f(x,y) в области Д и S площадь Д, тогда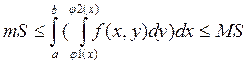

3)  Двукратный интеграл от непрерывной функции f по области Д с площадью S равен произведению площади на значение функции в которой точка p из Д.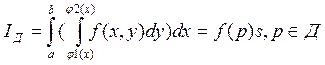

Вычисление двойного интеграла.

Теорема : двойной интеграл от непрерывной функции по правильной в направлении оси OY в Д равен двукратному интегралу по области Д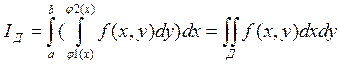

Доказательство.

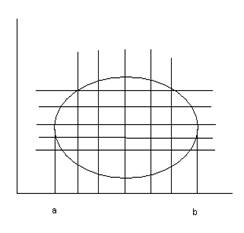
разобьем на n плоскостей  тогда

- интегральная сумма для f(x,y) по области Д.

 

повторный интеграл принято записывать в виде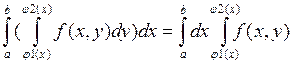

если Д правильная в направлении оси OX, ограничено линиями 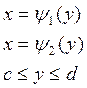, то повторный интеграл имеет вид: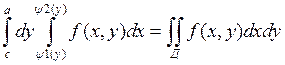

Если область Д является правильной ни в каком направлении, то её разбивают на конечное число правильных областей, вычисляют двойной интеграл по каждой из них и складывают. Теорема об оценке и о среднем также имеет место для двойного интеграла.

Двойной интеграл в полярной системе координат.

Точка О называется полюсом и заданная ось называется полярной осью

Совместим декартовую и полярную системы координат:

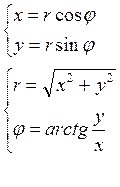
Пусть в полярной системе координат задана такая область Д, что каждый луч проходящий через внутреннюю точку области пересекает границу не менее двух раз.

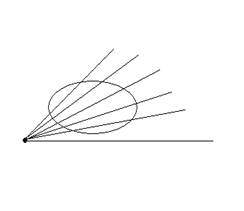
Такая область называется правильной в полярных ординатах. Путь Д ограничена лучами  и линиями .

Пусть Д задана

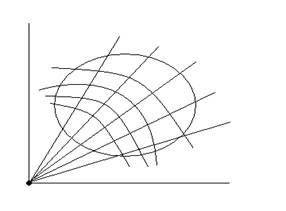
Разбиение области на площадки проводят с помощью лучей  и с помощью концентрических окружностей , где r₀ – наименьшее значение функции .  - площадка ограниченная линиями

Суммируем площадки ограниченные двумя соседними лучами, а потом собираем остальные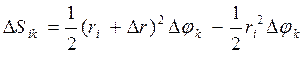

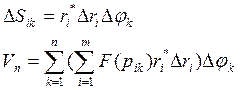
 тогда внутренняя сумма в пределе будет стремится к интегралу 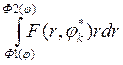 пусть  тогда  сумма будет стремится к интегралу по  и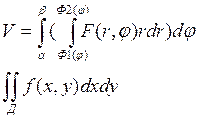

Если Д правильная в полярных координатах область, то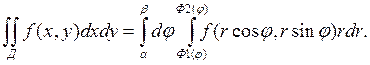

Вычисление площади и объёма с помощью двойного интеграла.

Объем тела V ограниченного поверхностью z=f(x,y),f(x,y)0, плоскостью z=0 и цилиндрической поверхностью с направляющей границы области Д, а образующие параллельны оси OZ по определению двойного интеграла считается по формуле

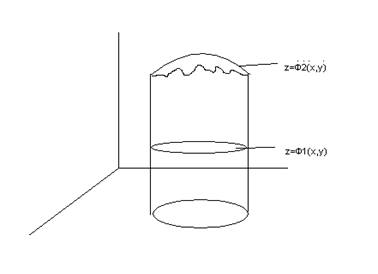
Замечание: если сверху тело ограничено поверхностью , а снизу  причём проекции обеих поверхностей на плоскости XOY является Д, то объём считается по формуле

Площадь: Составим интегральную сумму для f(x,y)=1

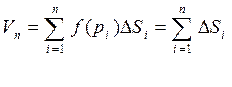
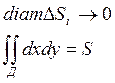
Тройной интеграл.

Пусть в пространстве задана область V ограниченная замкнутой поверхностью  и пусть в V определена и непрерывная функция f(x,y,z) разобьем V произвольным образом на области  выберем точку  и составим интегральную сумму: . Если существует предел интегральных сумм при diam который не зависит ни от способа разбиения области V ни от выбора точек , то этот придел называется тройным интегралом от функции f(x,y,z) по области V

Троекратный интеграл.

Пусть область V ограничена замкнутой поверхностью  обладает свойствами:

1)  Всякая прямая параллельная оси OZ и проведенная через внутреннюю точку области пересекает  в двух точках

2)  Область V проектируется на плоскость XOY в правильную область V.

3)  Всякая часть области V отсеченная плоскостью параллельной любой из координатных плоскостей также обладает 1 и 2 свойствами, и называется правильной трехмерной областью.

Дана правильная трехмерная область V ограниченная сверху , а снизу  и пусть f(x,y,z) определена непрерывна в области V, Д проекция области V на XOY и она ограничена линиями  тогда трехмерным интегралом называется интеграл: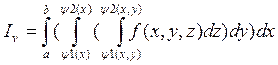

Свойства:

1)  Если область V разбить на две области плоскостью параллельной  какой либо из координатных плоскостей то троекратный интеграл по области V равен сумме троекратных интегралов.

Следствие: при любом разбиении V на конечное число областей плоскостями параллельными координатным плоскостям справедливо равенство

2)  Если m и M минимальное и максимальное значения функции f(x,y,z) в области V, то троекратный интеграл заключен  где V объем данной области.