Система дифференциальных уравнений. Задача Каши. Нормальные системы ЛОДУ с постоянными коэффициентами, страница 8

2.Пусть а находится в нутрии контура и при обходе контура С а остается слева, тогда по теореме Каши величина интеграла не зависит от выбора контура Св качестве контура можно взять окружность (a,r). Уравнение окружности:   ,

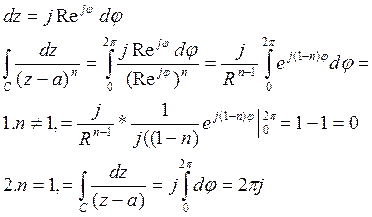
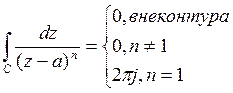
Интегральная формула Каши.

Пусть функция f(z) аналитична в односвязной области G и на границе Г  ограничивающая эту область, и пусть z любая точка области G.

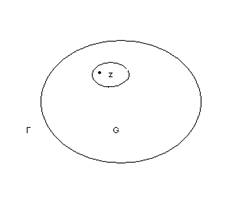
Опишем из центра z окружность  радиусом ,так чтобы  целиком лежала в нутрии области G. Опишем из центра z окружность , тогда

Так как f(z) аналитична, то при столь угодно молом  и достаточно малом  для любой точки  на

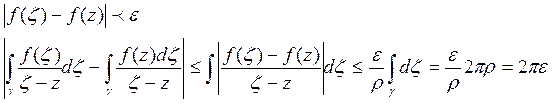
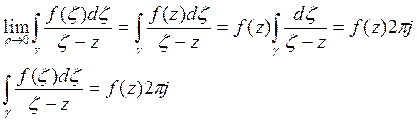
 - интегральная формула Каши.

Если точка z лежит не в области G, то в силу теоремы Каши:

Можно доказать используя интегральную формулу Каши. 

Интеграл типа Каши.

 - правая часть называется интеграл Каши.

 - замкнутый контур, f(z) – аналитична. Интеграл Каши определяет функцию, которая совпадает с f(z) в нутрии области G и равна 0  вне области G. Пусть Г – кусочно-гладкая дуга или совокупность таких дуг, f(z) – задана только на контуре и непрерывна на нём. Тогда  - называется интеграл типа Каши.

Тогда F(z) определена интегралом типа Каши, определена и не прерывна всюду кроме дуги С. И в любой Z не лежащей не дуге С, интеграл типа Каши имеет производную

 - причем производная есть аналитическая функция в любой точке не лежащей на дуге.

Степенной ряд с комплексными членами.

(1)  - степенной ряд,  - комплексная переменная.

Говорят что на некотором множестве G ряд (1) можарирует, если существует сходящийся числовой ряд такой, что во всех точках множества

В этом случае ряд (1) называется правильно сходящимся на G.

Ряд (1) сходится абсолютно если сходится ряд составленный из модулей его членов.

Из правильной сходимости ряда следует его абсолютная сходимость.

Правильно сходящиеся ряды можно почленно интегрировать и дифиринциравать и сумма ряда есть аналитическая функция.

Теорема Абеля: если степенной ряд (1) сходится в точке , то он сходится абсолютно при всех точках z таких что , при этом во всяком круге  ряд сходится правильно

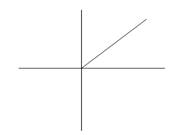
1.Ряд (1) сходится во всех точках этого луча.

2.Ряд (1) расходится во всех точках этого луча кроме точки 0. В точке 0 ряд сходится и сумма ряда равна .

3.На луче существуют как точки сходимости, так и точки рассходимости ряда.

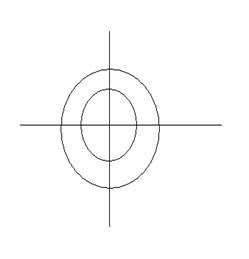
Из теоремы Абеля следует, что всякая точка сходимости находится ближе к 0 точке, чем всякая точка рассходимости: существует  определяющая точки сходимости от точек рассходимости. Причем  принадлежит и к одному и к другому множеству. Ряд (1) будет сходиться внутри G с центром в 0 и расходится вне этого круга. G – круг сходимости степенного ряда, а его радиус называется радиусом сходимости.

 (2)

Ряд (2) где а комплексное число также называется степенным рядом. Его областью сходимости является круг с центром в точке Q.

Ряд Тейлора.

Пусть f(z) аналитична внутри G ограничена окружностью С с центром в точке а.

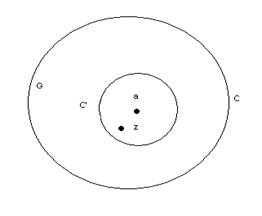
Проведем окружность С' так, чтобы z оказалась внутри С'.

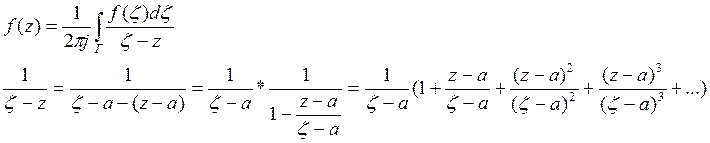
Прогрессия  является правильно сходящимся рядом, потому что она можарируется числовым рядом:

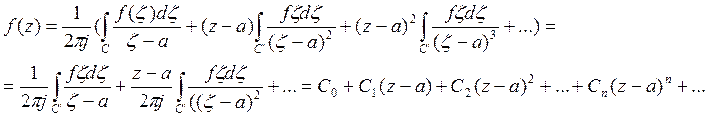
где

…

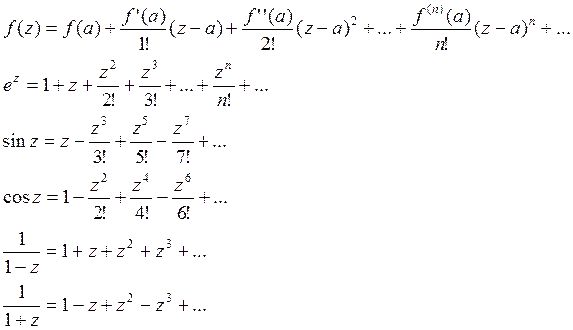
Ряды Тейлора могут сходиться и в функциях, где точка не определена, тогда в такой точке значение равное сумме её ряда Тейлора.

Радиус сходимости ряда Тейлора для всякой элементарной функции равен расстоянию от точки, а до ближайшей особой точки.

Нули аналитической функции.

Если f(a)=0, то точка а называется нулем функции f(z).

Ряд Тейлора имеет вид:

Если в разложении в ряд Тейлора

, т.е. ряд имеет вид: , то  точка а называется нулем функции f(z) порядка n или кратности n. Если n=1 ноль называют простым.

Продиффиринцируем последнюю формулу:

 получим что точка а является 0 порядка n-1 для f'(z).

, где .

Теорема: всякая функция вида , где  n – целое положительное число и  - аналитична в а и имеет в этой точке 0 порядка n.

Ряд Лорана.

Пусть f(z) однозначная аналитическая функция внутри кольца между окружностями С' и C" с центром в точке а.