Система дифференциальных уравнений. Задача Каши. Нормальные системы ЛОДУ с постоянными коэффициентами, страница 7

Если существует придел отношения  по любому закону, то этот предел называется производной f(z) в точке z.

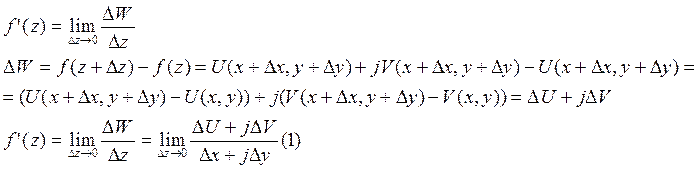
Пусть f(z) имеет производную, тогда lim (1) существует и не зависит от способа строения.

Пусть , тогда от точки  и z идем по прямой параллельной оси OX

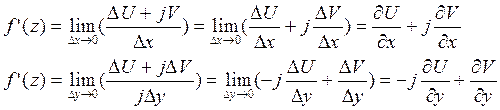
По определению производной предел не должен зависеть от способа стремления , поэтому

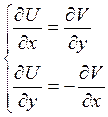- это условия Каши-Ремана.

Они должны быть выполнены в любой точке в которой функция дифиринцируема. Если частные производные  непрерывны в точке с координатами (x,y), то условие Каши-Ремана не только не обходимы, но и достаточны для дифиринцирования функции f(z).

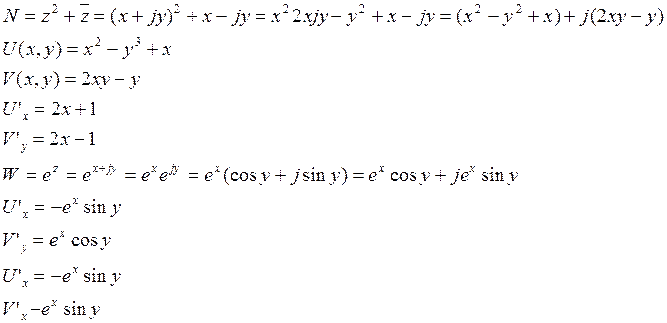
Значит функция дифиринцируема

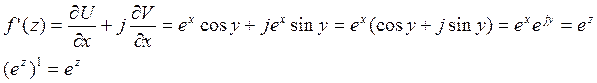
Если функция дифиринцируема не только в точке но и в её окрестности, то она называется аналитической в данной точке.

Функция аналитическая во всех точках некоторой области называется аналитической в этой области. Точки плоскости z в которых функция f(z) является аналитической называются правильными точками этой функции. А точки в которых f(z) не является аналитической – особыми.

1. Точки в которых f(z) неопределенны относятся к особым.
2. Для аналитической функции все известные правила дифиринцирования имеют место.

Теорема: Действительная и мнимая часть аналитической функции f(z)=U(x,y)+j(x,y) являются в области аналитичности гармоническими функциями, т.е. удовлетворяют уравнению Лапласа: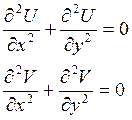

Доказательство.

Выпишем условия Каши-Ремана для аналитической функции:

        

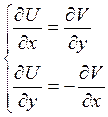
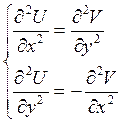
Две гармонические функции U(x,y) и V(x,y) удовлетворяют условию Каши-Ремана и являются действительной и мнимой частью аналитической функции f(z) называются сопряженными. Если задана одна из этих двух функций, то сопряженная к ней функция определяется с помощью криволинейного интеграла двумя своими частными производными из условия Каши-Ремана с точностью до константы.

Интеграл от функции комплексного переменного.

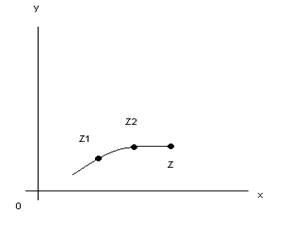
На плоскости комплексного переменного С задана дуга С, где z – кусочно-гладкая кривая с граничными точками . Пусть на С задана f(z) разобьем на n элементарных дуг точками

 - длина хорды стягивающая i  дуги на каждой элементарной дуге . Выберем точки  и составим интегральную сумму .

Если существует предел интегральной суммы при .

И этот предел не зависит ни от способа разбиения дуги Z ни от выбора точек , то он называется интегралом от f(z) по дуге С.

Свойства :

1.

2.  k – комплексная константа.

3. Если  тоже дуга что и С но с противоположным направлением то

4. Если дуга С состоит из дуг , то

5.

Доказательство.

Рассмотрим интегральную сумму если f(z)=1, тогда

5. Если  во всех точках дуги С, то

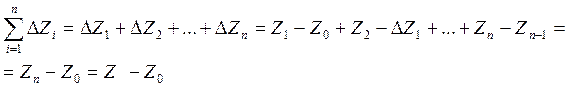
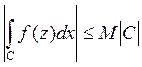
Вычисление интеграла от функции комплексного переменного.

1.Пусть z=x+jy

F(z)=U(x,y)+jV(x,y)

Dz=dx+jdy

f(z)dz=(U+jV)(dx+jdy)=Udx+jVdy-Vdy=(Udx-Vdy)+j(Vdx+Udy)

    

2.В случае если дуга С задана параметрически

, тогда

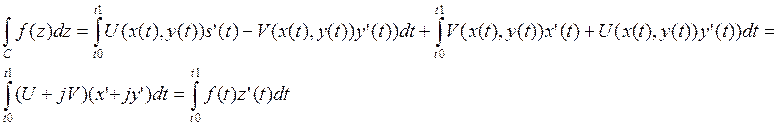
Теорема Каши.

Теорема: пусть f(z) аналитическая функция односвязной области G ограниченной контуром С, тогда

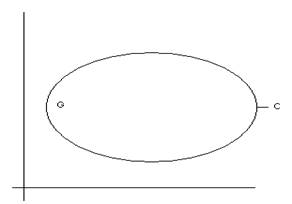
Доказательство.

Так как f(z) аналитическая функция, то она имеет производную, то её действительная и мнимая части удовлетворяют условию Каши-Ремана:

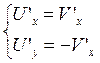
Рассмотрим каждый интеграл по отдельности. Условия выполняются так, как они совпадают с условиями Каши-Ремана.

Пусть теперь G многосвязная область ограниченная внешним контуром  и внутренними контурами  и пусть f(z) аналетична в G и на контурах.

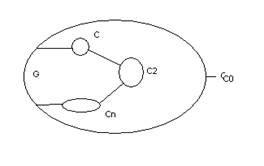
Обозначим .

Соединим контуры дугами . Область разбивается на две области с границами  и  

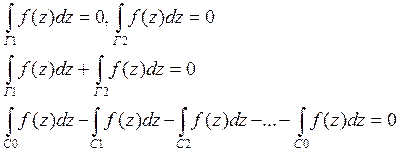
Интегралы по дугам уничтожаются так, как дуга проходит два раза в разных направлениях.

- теорема Каши для составного контура

Следствие: если f(z) аналитична на контурах  и  и в области ограниченной этими контурами, то .

Вычисление интеграла.

, где n – целое число

1.Пусть точка z=a находится в контуре С и вне области ограниченную этим контуром, тогда по теореме Каши: .