Система дифференциальных уравнений. Задача Каши. Нормальные системы ЛОДУ с постоянными коэффициентами, страница 12

 - скорость движения точки

 - ускорение.

Предположим:

1.Струна абсолютно гибкая.

2.Струна упругая – выполняется закон Гука.

3.Струна однородная с плотностью .

Рассмотрим только малые колебания струны: такие что если

 - острый угол между OX и касательной струны

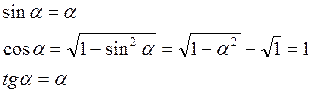
Так как , то

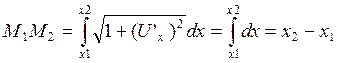
При сделанных предположениях можно пренебречь изменением длины любого участка струны.

Покажем что при предположениях Т постоянна и не зависит ни от времени ни от точек её приложения.

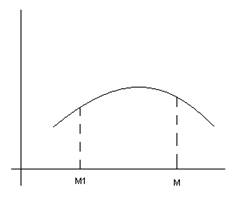
Так как по условию все точки струны движутся параллельно оси OY, а внешние силы так же параллельны ей, то сумма проекций сил натяжения на ось OX должна быть равна нулю.

 из-за произвольности выбора точек  и  следует, что сила натяжения Т не зависит от точки и в данный момент времени илы натяжения во всех точках равны. По закону Гука .

Замечание:

Сила натяжения Т направленная по касательной. Пусть малый участок   проецируется в интервал .

Проецируем на ось OX:

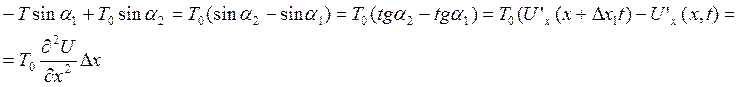
Применим второй закон Ньютона:

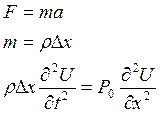
-уравнение колебания струны или одномерное волновое уравнение.

Оно описывает свободные колебания струны без внешних усилий.

Это уравнение имеет бесконечно много решений U(x,t) должно удовлетворять граничным условиям, т.е. в точках x=0 и x=e и начальным условиям, описывающим состояние струны в начальный момент времени t=0. Совокупность начальных и граничных условий называются краевыми условиями. Пусть концы струны закреплены не подвижно, тогда граничными условиями будут U(0,t)=0, U(l,t)=0. Пусть в начальный момент времени струна имеет некоторую форму f(x), тогда U(x,0)=f(x) – начальные условия и в начальный момент времени известна скорость в каждой точке струны

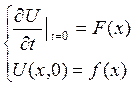 - начальные условия.

Замечание:

Если f(x)=0 и F(x)=0, то струна находится в покое, т.е. U(x,t)=0.

Метод Фурье.

Отыскиваем частные решения уравнения  удовлетворяющее краевым условиям: U(0,t)=0

U(l,t)=0

И начальным условиям

В виде:

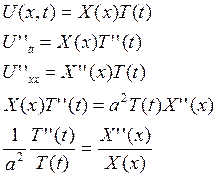
Так как левая часть зависит только от t, а правая только от х, то равенство справедливо только тогда, когда в левой и правой части стоят константы:

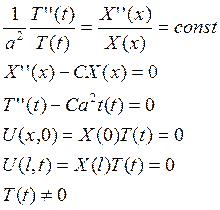
Получим:

Для X(x):

 - Задача Каши.

Случаи:

1)

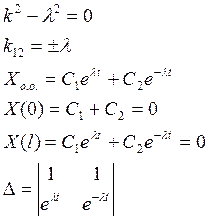
Система имеет единственное решение, а так как система однородная, то это решение нуль.

2) Пусть С=0

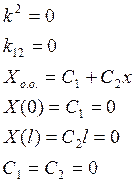
3) С<0

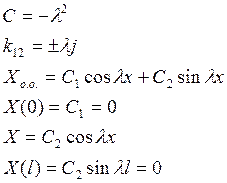
 или

  

.

Число  называется собственным числом, а функции  называется собственными функциями.

Замечание: Система собственных функций ортагональная на отрезке .

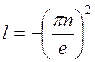
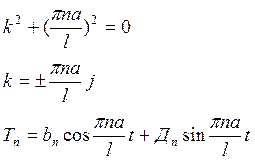
Тогда решение  функции  называются собственными функциями задачи колебания струны, а соответствующие им колебания собственными колебаниями.

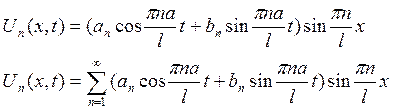
Подберем постоянные  и  так чтобы функция удовлетворяла начальным условиям.

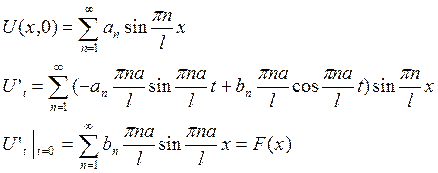
Величины  и  - есть коэффициенты разложения в ряд Фурье по синусам функций f(x) и F(x) на отрезке , поэтому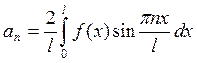

.

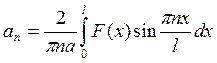Физический смысл собственных функций.

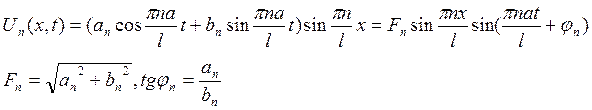
Все точки струны совершают гармонические колебания с одной и той же частотой  и фазой, амплитуда зависит от положения точки на струне и равна . Все точки струны одновременно достигают своего максимального отклонения и одновременно проходят положение равновесия. Такие колебания называются стоячими волнами.

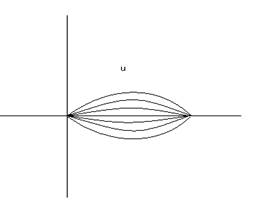
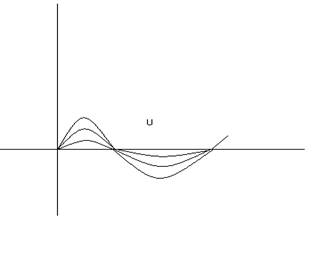
 имеет столько неподвижных точек сколько корней имеет уравнение  , а уравнение имеет n+1 корень с абсциссами .

Неподвижные точки называются узлами стоячей волны. Посередине узлов есть точки в которых отклонение достигает максимума, они называются пучностями. Любая струна имеет собственное колебание лишь строго определенных частот. Наименьшая собственная частота 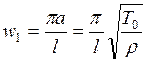. Высота звука возрастает с частотой колебания , самый низкий звук при , звук тем выше чем короче и легче струна и чем больше напряжение.

Тона, соответствующие частотам  называются гармониками.

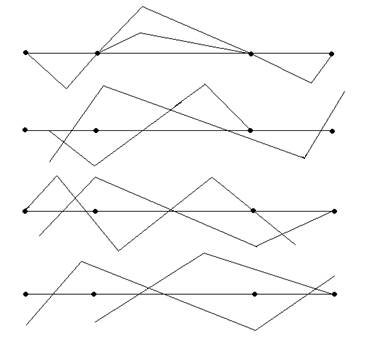
Если число n таково, что для некоторого , т.е. узел n – ой гармоники, то .

Пусть , то 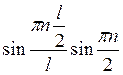. При n четных  является узлом. Амплитуда k – ой гармоники пропорциональна величине .