Система дифференциальных уравнений. Задача Каши. Нормальные системы ЛОДУ с постоянными коэффициентами, страница 4

3)  Троекратный интеграл  от f(x,y,z) по области V равен произведению объёма области V на значение функции в некоторой точке p в объёме V.

Доказательство.

По предыдущему свойству справедливо: 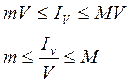т.е.  заключено между наименьшим и наибольшим значением функции. Поэтому по теореме о непрерывности функции существует P из V что =f(p).

Вычисление тройного интеграла.

Теорема: Тройной интеграл от функции  по правильной области V равен трехкратному интегралу по той же области: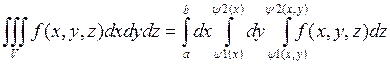

Доказательство.

Разобьем V плоскостями параллельными координатным плоскостям на n плоскостей тогда по 1 свойству

Каждая

 где  а это есть интегральная сумма для тройного интеграла.

Вычисление объёма тела с помощью тройного интеграла.

Пусть функция f(x,y,z) тождественно равна 1 в области V, тогда тройной интеграл по области V выражает объем этой области

Тройной интеграл цилиндрических координат.

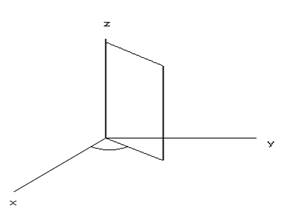
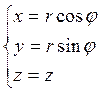
Область V разбиваем на элементарные объемы поверхностями

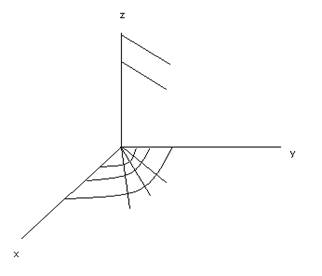
или с точностью до величины более высокого порядка малости

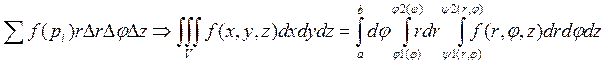
Тройной интеграл в сферических координатах.

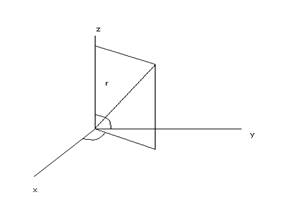
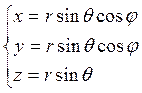
Тройной интеграл в сферических координатах имеет вид:

Координаты центра масс.

Пусть есть точка  и масса Статическим моментом этой точки относительно плоскости  называется произведение .

Если точек несколько то статистический момент нескольких точек . Если масса распределена по некоторой области g, то статистический момент тела g относительно  считается по формуле:  в двумерном случае:  , - координата центра тяжести,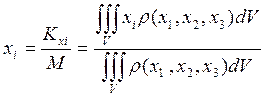

Если тело плоское то тройной интеграл заменяется на двойной.

Теория поля.

Криволинейный интеграл.

Пусть в каждой точке  поставлен вектор  говорят что в области задано векторное поле.

Пусть на плоскости задана линия L и две точки M и N и на линии задано векторное поле . F – это сила под действием которой материальная точка движется по линии L. Требуется найти работу этой силы при движении точки из M в положение N.

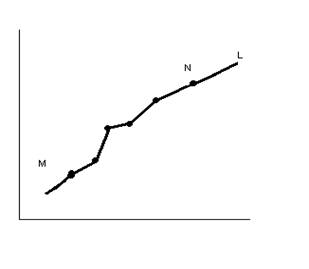
Разобьём кривую L на n произвольных частей точками:   

, тогда работа силы  при движении вдоль вектора :  где точка  тогда

Если существует предел при  и этот предел не зависит от способа разбиения кривой L, ни от выбора точек , то такой предел называется криволинейным интегралом и обозначается

В криволинейном интеграле учитывается направление от точки M к точке N которое называется направлением интегрирования.

Свойства:

1. Криволинейный интеграл определяется подынтегральным выражением, формой кривой интегрирования. При изменении направления интегрирования криволинейный интеграл меняет знак.

2. Пусть кривая L разбита точкой К на две прямые  и  тогда криволинейный интеграл  это соотношение справедливо для любого конечного числа слагаемых.

Пусть криволинейный интеграл задан в пространстве тогда  и вектор .

 если криволинейный интеграл от вектора  берётся по замкнутой кривой, то этот интеграл называется циркуляцией вектора  по контуру. .

Вычисление криволинейного интеграла.

Пусть L задана параметрически   тогда  

=

Формула Грина.

Пусть контур L замкнут и ограничивает область D

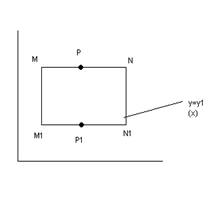
||OY

||OY

Пусть в Р заданы непрерывные функции P(x,y) и Q(x,y) имеющие непрерывные частные производные.

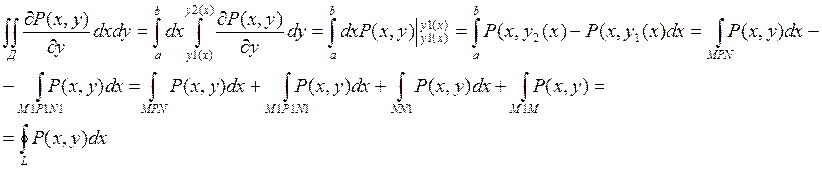
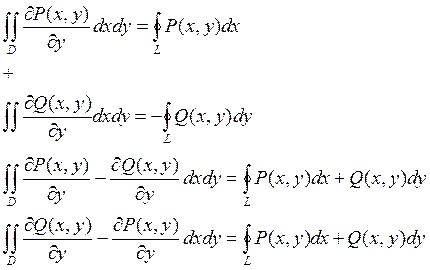
Условие независимости криволинейного интеграла от пути.

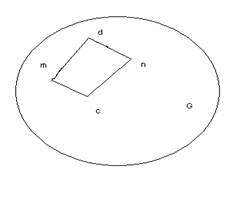
Пусть на плоскости XOY есть некоторая область G и точки M и N принадлежат G.

Теорема: для того чтобы криволинейный интеграл по кривой соединяющей любые две точки M и N некоторой области G не зависел от формы соединяющей их кривой, а зависел только от их положения необходимо и достаточно чтобы криволинейный интеграл по любому замкнутому контуру был равен нулю.

Доказательство.

Пусть криволинейный интеграл по любому замкнутому контуру равен нулю:

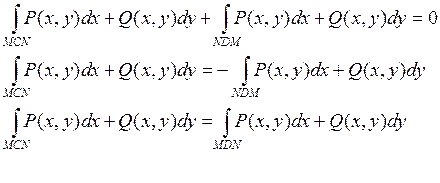
Пусть интеграл не зависит от пути:

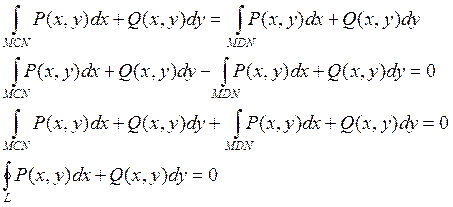
Пусть во всех точках некоторой области G функции P(x,y) и Q(x,y)  и  непрерывны, тогда для того чтобы криволинейный интеграл по замкнутому контуру L лежащему в области G был равен нулю необходимо и достаточно чтобы во всех точках области G выполнилось равенство: