Система дифференциальных уравнений. Задача Каши. Нормальные системы ЛОДУ с постоянными коэффициентами, страница 9

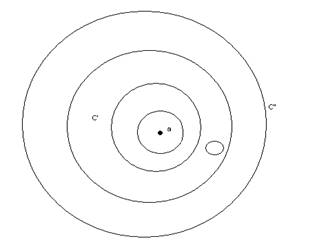
Проведем окружности Г' и Г" чтобы С оказалась между ними. Опишем из z как из центра окружность  целиком лежащую между Г' и Г".

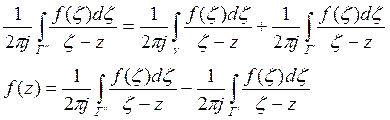
Так как  лежит на Г" то (z-a)<( -a) и

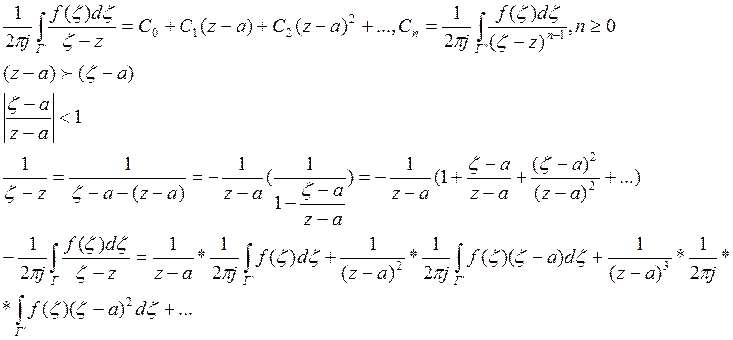
 - Разложение функции в ряд Лорана.

Г – любая окружность с центром в а лежащая внутри кольца.

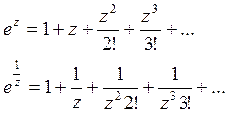
1)

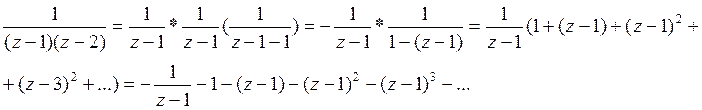
2)

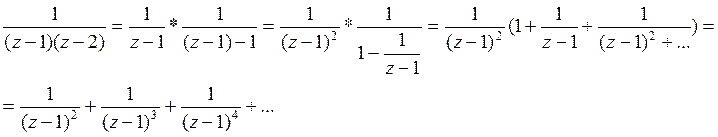
Таким способом находят разложение в ряде Лорана любой рациональной дроби.

Дробь  рассматривают как сумму бесконечно убывающей геометрической прогрессии, а дробь  как сумму ряда полученного путем k-1 кратного диффиринцирования геометрической прогрессии.

Изолированные особые точки.

Особая точка функции f(z) называется изолированной, если в её окрестности нет других особых точек функции.

Разложение функции в ряд Лорана, сходящийся во всех точках круга с центром в точке а кроме самой точки а называется разложением функции в ряд Лорана в окрестности, данной изолированной особой точки:

(1)  - правая часть ряда Лорана

(2)  - главная часть ряда Лорана

1)Пусть в окрестности изолированной особой точки z=a  ограничена.

В качестве контура Г формула для  возьмём окружность с радиусом R и центром

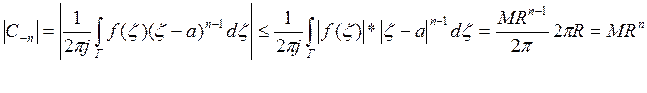
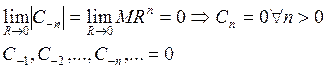
Получим, что главная часть ряда Лорана отсутствует, ряд состоит только из своей правильной части, поэтому он сходится не только в окрестности точки а, но и в самой точке а.

Если , то точка а перестанет быть изолированной особой точкой f(z), а станет её правильной точкой. а называется устранимой особой точкой.

                              

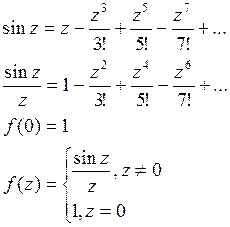
Пусть f(z) не ограничена в окрестности изолированной особой точки а, если

, то а называется полюсом функции f(z).

Если же при  функция f(z) не имеет предела ни конечного ни бесконечного, то а называется существенно особой точкой.

Пусть z=a полюс f(z)

 в некоторой окрестности а.

Рассмотрим  - функция аналитическая.

, т.е. является нулём функции F(z).

Точка z=a называется полюсом порядка n функции f(z) если она является 0 порядка n функции . При n=1 полюс называется простым.

- аналитическая.

, где  и - аналитическая в окрестности точки а.

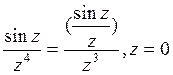- полюс 3 порядка.

, -простые

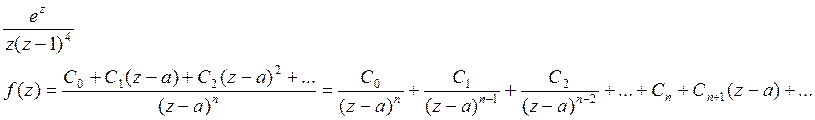Если полюс порядка n функции f(z), то главная часть разложения этой функции в ряд Лорана в окрестности точки а есть не , а конечная сумма причем порядок полюса равен наивысшему показателю (z-a) в знаменателях.

Главная часть разложения функции в ряд Лорана в окрестности существенной особой точки содержит бесконечное число отличных от нуля членов.

Бесконечно удаленная особая точка.

Добавим в плоскости комплексного переменного 1 несобственный элемент называющийся бесконечно удаленной точкой.

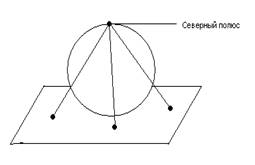
Окрестность бесконечно удаленной точки называется внешность круга с центром в нуле.

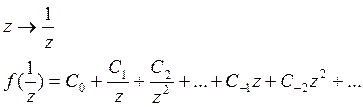
Заменой z на  изучение функции f(z) сводится к изучению функции , поэтому

- называется правильной частью

- называется главной частью рада Лорана.

Если в некоторой окрестности бесконечно удаленной точки f(z) ограничена, то

, а разложение , тогда бесконечно удалённую точку можно считать правильной точкой предположив: .

Если , то будем называть бесконечность нулевого порядка n, если z=0 является нулевым порядком n

Если , то тогда бесконечный полюс функции и его порядок такой же как у точки t=0 функции .

Разложим ряд Лорана:

Если  не существует, то бесконечно удаленная точка называется существенно особой точкой и главная часть ряда Лорана содержит бесконечное число отличных от нуля членов.

Вычеты.

Пусть точка а является правильной или изолированной особой точкой функции f(z) и контур С таков что на всем контуре и внутри него f(z) аналитична, кроме самой точки а. Величина  называется вычетом функции f(z) относительно точки а. Вычет обозначается: .

Если точка а правильная, то по теореме Каши получаем, что .

Первый  коэффициент главной части ряда Лорана () в окрестности точки а функции f(z) считается по формуле:

.

Теорема: Основная теорема о вычетах: пусть  замкнутый контур, на котором функция f(z) аналитична. Пусть f(z) также аналитична внутри  за исключением n изолированных особых точек, тогда  равняется сумме вычетов функции f(z) относительно всех особых точек функции находящихся внутри контура :