Система дифференциальных уравнений. Задача Каши. Нормальные системы ЛОДУ с постоянными коэффициентами, страница 10

.

Доказательство.

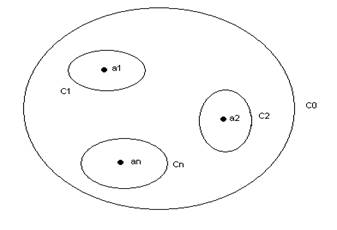
Окружим точки  окружностями столь малого радиуса, чтобы внутри каждой окружности находилось по одной особой точке f(z) и чтобы никакие две окружности не пересекались, тогда по теореме Каши:

По определению вычета:

.

Вычетом f(z) относительно бесконечно удаленной точки называют величину , где С – окружность с центром в 0, столь большого радиуса, что вне этой окружности нет особых точек, функции отличных от бесконечно удаленной особой точки и направление интеграла по z выбирается по часовой стрелке поэтому

Пусть f(z) имеет конечное число особых точек, тогда всех их можно поместить внутрь круга большого радиуса с центром в нуле.

По основной теореме о вычетах:

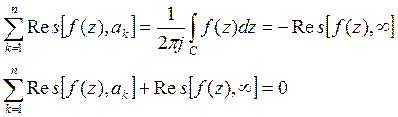
Сумма вычетов функции относительно всех её особых точек, включая бесконечно удаленные точки, равна нулю.

Вычет относительно полюса.

Если точка а является простым полюсом f(z), то в окрестности этой точки ряд Лорана имеет вид: , где -правильная часть ряда Лорана, она аналитична и непрерывна.

Выразим :

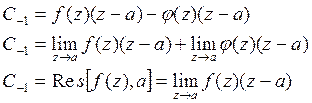
Пусть, а простой полюс и , где функции  и  аналитичны в а, :

.

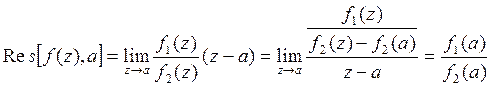Пусть точка а является полюсом порядка m для f(z), тогда в окрестности точки а ряд Лорана имеет вид: , где  - правильная часть ряда Лорана, аналитическая функция.

Умножим обе части на , получим:

Продиффиринцируем m-1 раз получим:

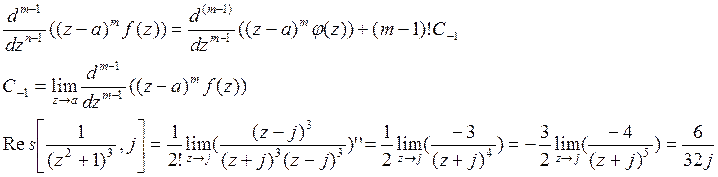
Операционное исчисление.

Преобразования Лапласа и его связь с преобразованием Фурье.

 - является кусочно-гладкой

1. f(t) и f'(t) определены всюду и непрерывны на любом конечном интервале кроме конечного числа точек разрыва 1 рода.

2. f(t) – абсолютно интегрируема

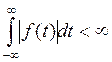, тогда f(t) представима в комплексной форме

, где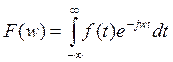

F(w) – спектральная плотность или преобразования Фурье f(t).

Если речь идет о реальном физическом процессе, то есть о моменте времени и дальше процесс продолжается длительное время, теоретически , поэтому для реального процесса преобразования Фурье:

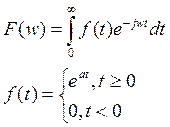
Рассмотрим затухающую функцию  и составим для неё спектральную плотность:

(1) (2)

(1) Интеграл Лапласа

(2) Обращение интеграла Лапласа.

Переход от f(t) в F(p) называется преобразованием Лапласа. () , где p – комплексная переменная .

 и несобственные интегралы сходятся абсолютно. Преобразования Лапласа существуют для всех функций-оригиналов.

f(t) – называется оригиналом если:

1) f(t) определена при всех t, причем f(t)=0, t=0

2) f(t) является кусочно-гладкой

3) Существует C>0 и , такие что .

Если условие 3)выполнено при , то оно выполняется для всех .

Наименьшее число  для которого выполнено условие 3) называется индексом или показателем роста функции f(t) при .

Если f(t) функция оригинал с индексом роста , то полуплоскость  на плоскости комплексного переменного p называют полуплоскостью сходимости интеграла Лапласа.

Преобразования Лапласа функции оригинала называют её изображением.

Функцией Хевисайда называется следующая функция:

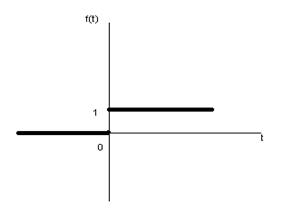
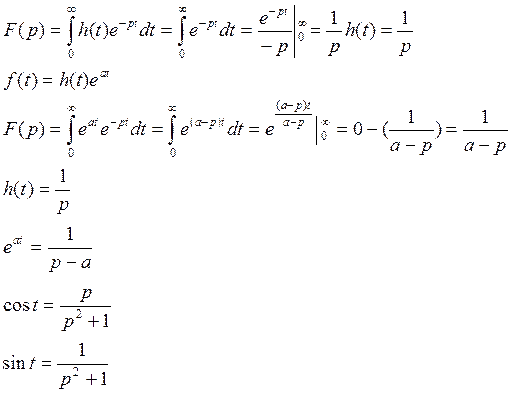
1)Если f(t) функция оригинал, то t*f(t) так же функция оригинал с тем же индексом роста .

2)Если f(t) функция оригинал с индексом роста , то интеграл Лапласа сходится абсолютно для всех p в полуплоскости сходимости, если же , то в полуплоскости , сходится абсолютно и равномерно.

3)Если f(t) функция оригинал с , то её преобразования Лапласа F(p) есть аналитическая функция во всей полуплоскости сходимости.

4)Теорема: если f(t) оригинал с индексом роста  и F(p) его изображение, то во всякой точке непрерывности f(t) выражается через изображение по формуле обращения:

.

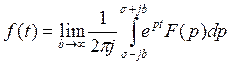Основные теоремы об оригиналах и изображениях.

Если f(t) функция оригинал такая, что кроме преобразования Лапласа существует и преобразование Фурье, то

Теорема: поведение изображения в бесконечности. Любое изображение F(p) стремится к нулю если

Доказательство.

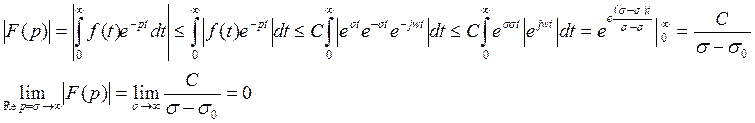
Замечание: обычно изображение есть рациональная функция, а она не имеет особенностей кроме полюсов, но из доказанного следует, что полюсов в бесконечности нет, поэтому бесконечность всегда является правильной точкой  и разложение в окрестности бесконечности имеет вид: .