Теорема: если f(t)=0,
то F(p)=0 и обратно: если F(p)![]() 0, то f(t)
0, то f(t)![]() 0.\
0.\
Теорема линейности: пусть ![]() и
и ![]() функции оригиналы с индексами роста
функции оригиналы с индексами роста![]() и
и ![]() ,
тогда для произвольных коэффициентов
,
тогда для произвольных коэффициентов ![]()
![]() имеет место соотношение:
имеет место соотношение:
![]() с полуплоскостью сходимости
с полуплоскостью сходимости ![]() .
.
Теорема диффиринцирование оригинала: если вместе с f(t) её производной является функцией
оригиналом, то ![]()
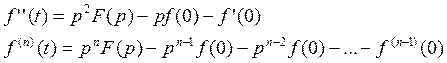
Доказательство.
По определению: 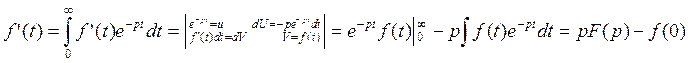 .
.
Теорема интегрирования оригинала: если f(t) функция оригинал, то 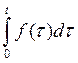 так
же функция оригинал и его изображение будет
так
же функция оригинал и его изображение будет ![]() .
.
Доказательство.
Обозначим 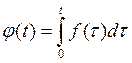 и покажем что эта
функция является функцией оригиналом. Пусть
и покажем что эта
функция является функцией оригиналом. Пусть ![]() ,
оценим
,
оценим
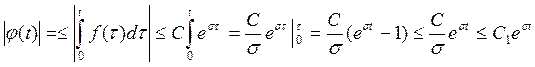
![]()
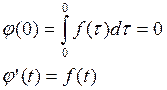
Переведем в изображение:
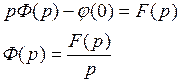
Теорема подобия: если ![]() произвольное
число, то
произвольное
число, то ![]()
Доказательство.
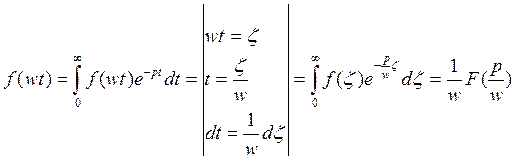
Теорема диффиринцирование изображения: если f(t)=F(p) и n натуральное
число, то ![]() .
.
Доказательство.
Выпиши формулу для F(p) и продиффиринцируем её:
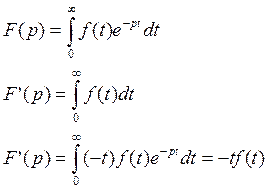
Теорема интегрирования изображения: если f(t)=F(p) и ![]() функция оригинал, то
функция оригинал, то 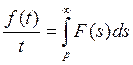 , где интегрирование производится по
кривой соединяющей точки p и
, где интегрирование производится по
кривой соединяющей точки p и ![]() в полуплоскости сходимости оригинала
в полуплоскости сходимости оригинала ![]() .
.
Доказательство.
Пусть 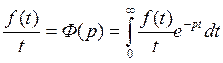
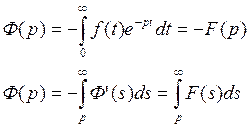
Свертка.
Пусть функция f(t)
и g(t) определены при всех t. Сверткой функции f(t) и g(t) называют
функции 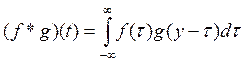 .
.
Свойства:
1)Операция свертки коммутативна, т.е. обе части равенства имеют смысл.
Доказательство.
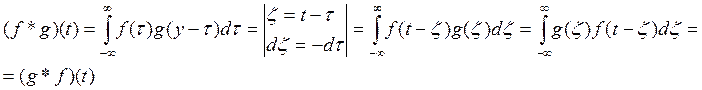
2)Для функций оригиналов f(t) и g(t) операция
свертки всегда выполнима причем 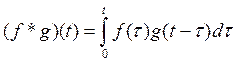 .
.
3)Свертка функции оригиналов f(t) и g(t) с
индексом роста ![]() и
и ![]() так
же функция оригинал, чей индекс роста не превосходит вилечены
так
же функция оригинал, чей индекс роста не превосходит вилечены ![]() .
.
Доказательство.
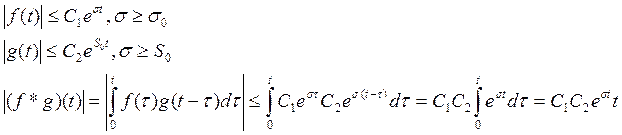
Теорема умножения: если f(t)=F(p) g(t)=G(p), то F(p)G(p)=(f*g)(t).
Доказательство.
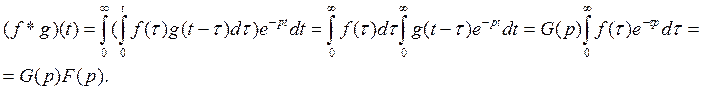
Теорема Дюамеля: если f(t) и g(t) и g'(t) функции оригиналы, то
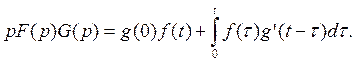
Доказательство.
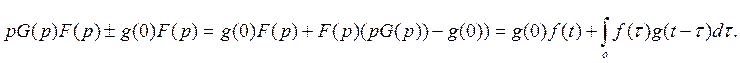
Изображение кусочно-линейной и периодической функции.
Кусочно-линейная:
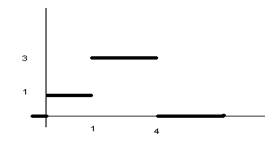
![]()
Пусть ![]() в точке разрыва
функции f(t) или f'(t).
в точке разрыва
функции f(t) или f'(t). ![]() -
скачек функции в узлах,
-
скачек функции в узлах, ![]() - скачек производной
в узлах стыка, тогда
- скачек производной
в узлах стыка, тогда ![]() .
.
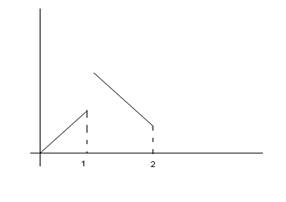
![]()
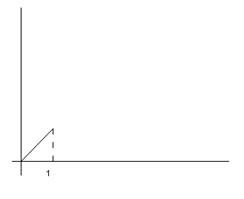
![]() .
.
Изображение периодической функции.
Пусть ![]() , где
, где ![]() - периодическая с периодом Т функция
- периодическая с периодом Т функция ![]() .
.
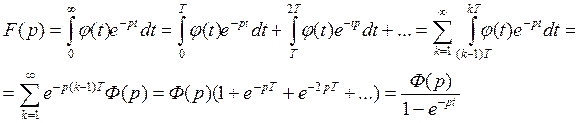
Нахождение оригиналов по изображению.
Если изображение ![]() дробно-рациональная
функция, то дробь раскладывается на простые дроби и для каждой простой дроби
оригинал находится по таблице или используя свойства
дробно-рациональная
функция, то дробь раскладывается на простые дроби и для каждой простой дроби
оригинал находится по таблице или используя свойства
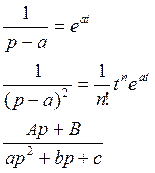
![]()
Теорема разложения: пусть F(p) имеет в бесконечности правильную точку причем его
разложение в окрестности бесконечности имеет вид: ![]() ,
тогда оригиналом является k(t)f(t), где
,
тогда оригиналом является k(t)f(t), где ![]() причем
ряд сходится при всех t.
причем
ряд сходится при всех t.
Теорема Жордана: пуст для ![]() бесконечность
правильная точка и
бесконечность
правильная точка и ![]() имеет на всей плоскости только
конечное число изолированных особых точек
имеет на всей плоскости только
конечное число изолированных особых точек ![]() .
.![]()
![]() дуга
окружности расположенная в полуплоскости
дуга
окружности расположенная в полуплоскости ![]() ,
тогда
,
тогда ![]() .
.
Вторая теорема разложения: если изображение есть
дробно-рациональная функция ![]() , то оригиналом
является
, то оригиналом
является ![]()
![]() .
.
Доказательство.
 .
.
Так как количество полюсов конечно, то все полюса находятся на большом расстоянии от нуля. Проведем прямую и дугу окружности такого радиуса что бы все полюса попали внутрь фигуры.
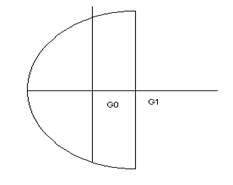
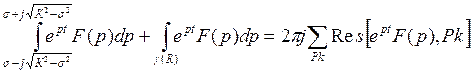
Устремим R к
бесконечности, тогда ![]() .
.
Применение операционного вычисления для ДУ.
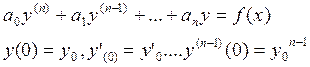
f(t) – функция оригинал.
y(t) – функция оригинал.
![]()
Пусть y(t)=Y(p), f(t)=F(p)
![]()
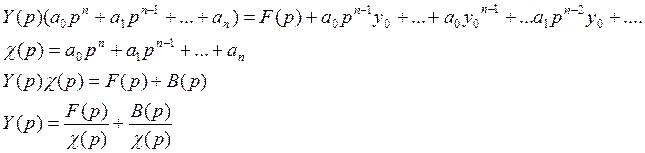
f(t) – входной сигнал
F(p) – изображение входного сигнала
y(t) – реакция или отклик системы на входной сигнал
Y(p) – операторный отклик
![]() - операторная проводимость или
передаточная функция.
- операторная проводимость или
передаточная функция.
![]() - характеристическое
уравнение.
- характеристическое
уравнение.
Пусть B(p)![]() 0, тогда
0, тогда ![]() -
операторный отклик равен умножению изображению входного сигнала на передаточную
функцию. Определить реакцию системы на различные входные сигналы при различных
начальных условиях.
-
операторный отклик равен умножению изображению входного сигнала на передаточную
функцию. Определить реакцию системы на различные входные сигналы при различных
начальных условиях.
![]()
V(t) – его решение, ![]()
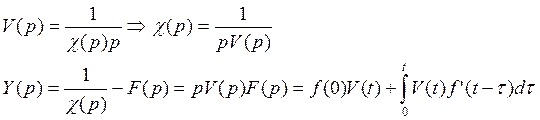
Аналогично операционным методом решают системы ДУ.
Уравнения математической физики.
Уравнения колебания струны.
XOU – система координат, U – отклонение струны от положения равновесия.
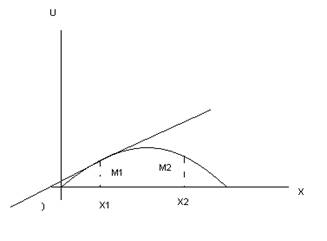
![]() , где х – абсцисса точки, t – время,
, где х – абсцисса точки, t – время, ![]() -
угловой коэффициент к графику в точке с абсциссой х. При любом фиксированном t U(x,t) – это положение струны в момент
времени t. При фиксированном х U(x,t) – закон движения точки с
абсциссой х вдоль прямой параллельной OY.
-
угловой коэффициент к графику в точке с абсциссой х. При любом фиксированном t U(x,t) – это положение струны в момент
времени t. При фиксированном х U(x,t) – закон движения точки с
абсциссой х вдоль прямой параллельной OY.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.