Рассмотрим замкнутый контур L из G.
![]() и следовательно криволинейный
интеграл по замкнутому контуру равен нулю.
и следовательно криволинейный
интеграл по замкнутому контуру равен нулю.
Пусть ![]()
Предположим противное: ![]()
Пусть в М из G ![]()
Т.к. производные функции непрерывные то их разность тоже непрерывная функция, поэтому разность будет так же положительная во всех точках некоторой малой окрестности D' содержащей точку М.
Рассмотрим ![]()
Наше предположение неверно.
Потенциал векторного поля.
Если во всех точках некоторой области М на плоскости задана
скалярная функция z=z(x,y) то говорят что в области задано
скалярное поле. Если же в каждой М некоторой области на плоскости поставлен в
соответствии вектор, ![]() то говорят что на плоскости
задано векторное поле.
то говорят что на плоскости
задано векторное поле.
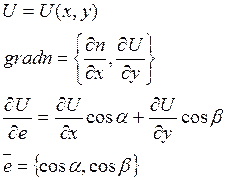
Векторное поле ![]() называется
потенциальным если оно является градиентом некоторой функции (
называется
потенциальным если оно является градиентом некоторой функции (![]() ). Функция U=U(x,y) называется
потенциалом векторного поля.
). Функция U=U(x,y) называется
потенциалом векторного поля.
Теорема: векторное поле ![]() потенциально
тогда и только тогда когда функции P и Q удовлетворяют условию:
потенциально
тогда и только тогда когда функции P и Q удовлетворяют условию: ![]()
Доказательство.
Необходимость: пусть существует потенциал такой что ![]() получим
получим
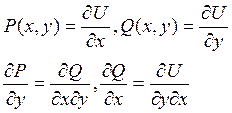
Достаточность: 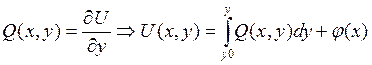
y0- ордината любой точки
плоскости в которой задано векторное поле. Подберём ![]() так
чтобы
так
чтобы ![]()
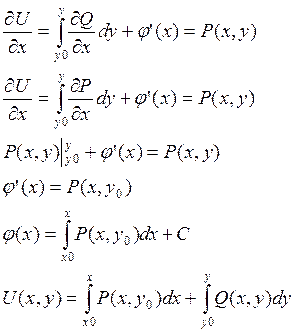
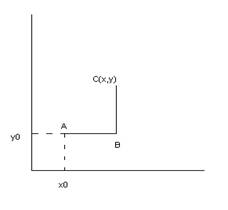
![]()
Поверхностный интеграл.
Касательная плоскость и нормаль к поверхности.
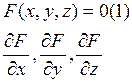
Прямая линия называется касательной к поверхности в некоторой точке P(x,y,z) если она является касательной к какой либо кривой принадлежащей поверхности и проходящей через P.
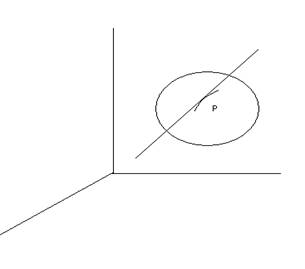
Теорема: пусть хотя бы одна из частных производных в точке P отлична от нуля, тогда все касательные к поверхности в точке P лежат в одной плоскости.
Такая плоскость называется касательной плоскостью поверхности 1 в точке P.
Прямая проведённая через P поверхности 1 перпендикулярна касательной плоскости называется нормалью поверхности. Направляющий вектор этой прямой называется вектором нормали к поверхности в точке P.
![]()
Определение поверхностного интеграла.
Пусть в пространстве задана поверхность, ![]() в каждой точке которой задано
положительное направление нормали и n единичный
вектор направляющие cos которого
есть непрерывная функция от (x,y,z).
в каждой точке которой задано
положительное направление нормали и n единичный
вектор направляющие cos которого
есть непрерывная функция от (x,y,z).
![]()
![]()
Пусть задано, ![]() где P,Q,R непрерывные функции. Разобьем поверхность,
где P,Q,R непрерывные функции. Разобьем поверхность, ![]() каким либо способом на элементарные
площадки
каким либо способом на элементарные
площадки ![]() i=1,2,…,n
i=1,2,…,n
На каждой площадке возьмем точку ![]() и
составим сумму
и
составим сумму ![]() (2) сумму называют
интегральной суммой.
(2) сумму называют
интегральной суммой.
Если существует предел интегральной суммы (2) при max размере ![]() и
этот предел не зависит ни от способа разбиения поверхности ни от выбора точек,
и
этот предел не зависит ни от способа разбиения поверхности ни от выбора точек, ![]() то он называется поверхностным интегралом
от скалярного произведения
то он называется поверхностным интегралом
от скалярного произведения ![]() и обозначается:
и обозначается:
![]()
![]()
Если ![]() есть скорость
жидкости то
есть скорость
жидкости то ![]() есть количество жидкости протекающей
через
есть количество жидкости протекающей
через ![]() в направлении
в направлении ![]() за
единицу времени, а поверхностный интеграл дает общее количество жидкости
протекающей через
за
единицу времени, а поверхностный интеграл дает общее количество жидкости
протекающей через ![]() в положительном направлении
нормали, поэтому поверхностный интеграл называется потоком векторного поля F через
в положительном направлении
нормали, поэтому поверхностный интеграл называется потоком векторного поля F через ![]() .
.
Если поверхность ![]() разбить на части
разбить на части ![]() то
то
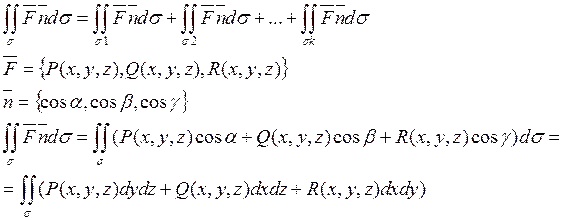
Формула Остроградского-Гауса.
Пусть в пространстве задана правильная трехмерная область V ограниченная ![]() и проектирующаяся в правильную область Д
в плоскости XOY.
и проектирующаяся в правильную область Д
в плоскости XOY.
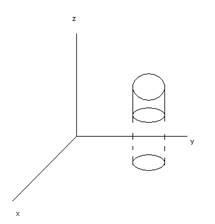
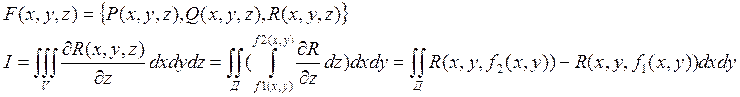
Рассмотрим внешнюю нормаль к поверхности ![]() .
.
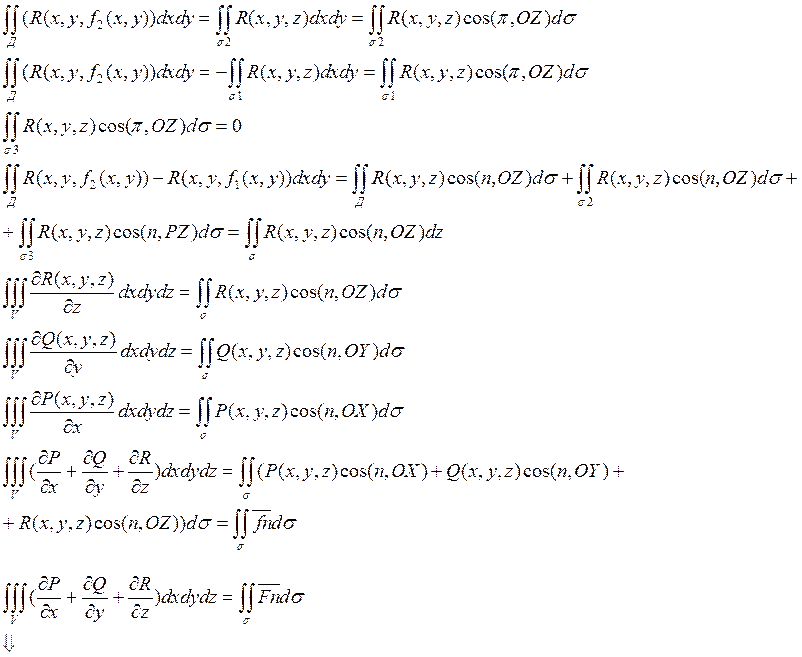 Формула Остроградского-Гауса.
Формула Остроградского-Гауса.
Определение дивергенции.
![]()
Дивергенцией векторного поля ![]() называется
выражение
называется
выражение ![]()
![]() - поток векторного поля через
замкнутую поверхность равен тройному интегралу от дивергенции поля по объему ограничивающую
эту поверхность.
- поток векторного поля через
замкнутую поверхность равен тройному интегралу от дивергенции поля по объему ограничивающую
эту поверхность.
С помощью теоремы о среднем для тройного интеграла и формулы
Остроградского можно дать другое определение дивергенции: 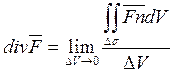 где
где ![]() -
объем бесконечно малой области содержащеё данную точку
-
объем бесконечно малой области содержащеё данную точку ![]() поверхность
ограничивающая этот объем, т.е. div является
плотностью потока векторного поля точки в которых
поверхность
ограничивающая этот объем, т.е. div является
плотностью потока векторного поля точки в которых ![]() -называется
источник, а
-называется
источник, а ![]() -называется сток.
-называется сток.
Формула Стокса.
Пусть в пространстве задана кривая L и поле ![]() . Причем P,Q,R непрерывны вместе со своими частными производными 1 порядка.
. Причем P,Q,R непрерывны вместе со своими частными производными 1 порядка.
Рассмотрим циркуляцию поля:
![]()
Ротором или вихрем поля ![]() называется
вектор:
называется
вектор:
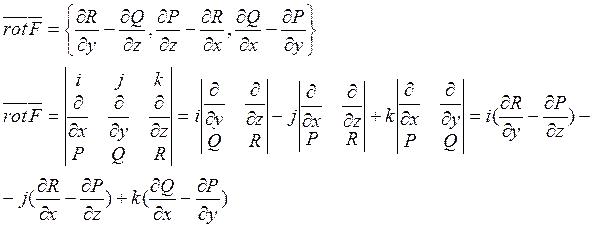
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.