Математическое планирование экспериментов. Планирование экстремальных экспериментов. Объект исследования, критерий оптимизации и факторы, страница 6

№№ п/п	хо	х1	х2	х3	Е1	Е2	`Е3	Е	Еп
1	2	3	4	5	6	7	8	9	10
1	+	+	+	+	89,5	89	90,5	89,7	89,5
2	+	-	+	+	91,5	92	91,5	91,7	96,7
3	+	+	-	+	85,5	86	84,5	85,6	85,5
5	+	+	+	-	92,5	91	91,5	91,7	91,9
6	+	-	+	-	94,5	95	93,5	94,3	94,1
7	+	+	-	-	88,5	87	89,5	88,3	88,0
8	+	-	-	-	90,5	90	89,5	90,0	90,2

Опыты выполнены по три раза и получены три колонки эффективности Е₁, Е₂, Е₃. Модель находим для среднего арифметического:

 

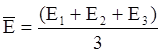
Находим линейную модель для средних значений:

  ;

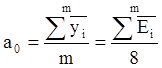Находим свободный член и коэффициенты при факторах:

 ;

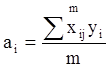а₀=( 89,7+91,7+85,3+88+97,1+94,3+88,3+90,8)/8=89,88

а₁=(89,7-91,7+85,3-88+91,7-94,7+88,3-90)/8= -1,12

а₂=(89,7+91,7-85,3-88+91,7+94,3-88,3-90)/8= 1,98

а₃=(89,7+91,7+85,3+88-91,7-94,3-88,3-90)/8= -1,20

Следовательно, получена модель (в условных единицах по факторам х_j)          Е=89,88-1,12х₁+1,98х₂-1,20х₃.

Из уравнения видно, что наибольший выход дает расход воды, причем с увеличением последнего значения Е возрастает, а с увеличением угла наклона грохота и частоты пульсаций эффективность падает.

Проведем анализ модели. Для этого найдем погрешность воспроизводимости каждого опыта по формуле

  ;

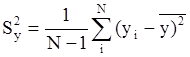S_в1²=( 89,5-89,7)²+(89-89,7)²+(90,5-89,7)²/(3-1)=(0,2²+0,7²+0,8²)/

/2=0,585;

S²_в2=(91,5-91,7)²+(92-91,7)²+(91,5-91,7)²/(3-1)=0,085

Аналогично          S²_в3=0,585;     S²_в4=0,25;       S²_в5=0,585;

S²_в6=0,585;     S²_в7=1,585;    S²_в8=0,25

Проверим по критерию Кохрена равнозначность дисперсий

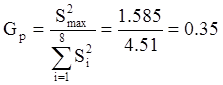
При числе сравниваемых дисперсий k=8 и числе степеней свободы сравниваемой дисперсии f_{s max}= 2 теоретическое значение G_т=0,54. Следовательно, G_p<G_т.

Погрешность отдельного результата в эксперименте

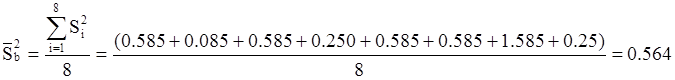
Погрешность средних значений

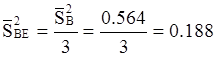
откуда

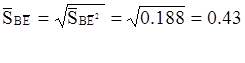
Проверим значимость коэффициентов. Для этого определим погрешность коэффициентов модели

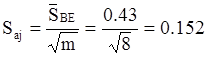
Находим предельно значимое значение коэффициентов

(a_j)_пред=tSa_j=2,12×0,152=0,32 , где t=2,12 найдем по таблицы критерия Стьюдента 95-процентной вероятности при числе степеней свободы f_в=16.

Поскольку все коэффициенты модели по абсолютной величине больше 0,32, все они значимы.

Проверим адекватность модели. Предсказываем по модели средний результат каждого опыта, для чего вместо х_j в модель подставим соответствующие опыту значения ±1:

Е_п1=89,88-1,12(+1)+1,98(+1)-1,20(+1)=89,54;

Е_п2=89,88-1,12(-1)+1,98(+1)-1,20(+1)=91,78;

Е_п3=89,88-1,12-1,98-1,20=85,58;

Е_п4=89,88+1,12-1,98-1,20=87,82;

Е_п5=89,88-1,12+1,98+1,20=91,94;

Е_п6=89,88+1,12+1,98+1,20=94,18;

Е_п7=89,88-1,12-1,98+1,20=88;

Е_п8=89,88+1,12-1,98+1,20=90,22

Записываем эти результаты в гр. 10 таблицы.

В гр. 11 разместим погрешность предсказания

DЕ=`Е-Е_н.

Число степеней свободы погрешности

f_ад=m-k-1=8-3-1=4.

Находим дисперсии неадекватности

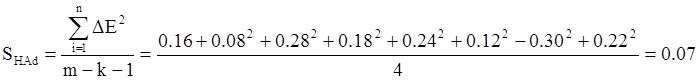
Остаточная дисперсия меньше дисперсии воспроизводимости, следовательно, не применяя критерия Фишера, можно утверждать, что модель адекватна.