Математическое планирование экспериментов. Планирование экстремальных экспериментов. Объект исследования, критерий оптимизации и факторы, страница 15

		I	II	III	j ® k
	1	A	B	C	Y1
¯	2	C	A	B	Y2
n	3	B	C	A	Y3
		YI	YII	YIII	Y
		YA	YB	YC

в котором I-III - конструкции импеллеров; 1-3 - типы собирателей;

A-C - типы вспенивателей.

Поставив девять опытов (по числу клеток в табл.4.12), получаем результаты по извлечению e и содержанию b :

e, %                                     b, г/т

87   83   84                       108   112   110

90   85   93                       105   110   100

92   80   88                       102   115   105   

Переходим к упрощенной форме записи результатов, вычитая из извлечения число 80, а из содержания число 100. Получим более удобные для расчетов результаты:                         

e, %                                     b, г/т

7   3    4                            8   12   10

10   5  13                            5   10     0

12   0    8                            2   15     5   

Подсчитываем суммы Y_I - Y_III ; Y₁ - Y₃ ; Y_A - Y_C  для отдельных условий и общую Y. Для извлечений этот расчет дает

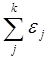= ; =7+10+12=29; =8; =25;

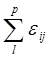= ;   =7+3+4=14;    =28;   =20;

= ;  =7+5+8=20;   =28;   =14;

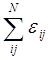= ;     =7+3+4+10+5+13+12+0+8 = 62.

Рассчитаем суммы квадратов:

.

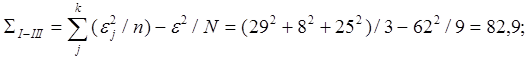
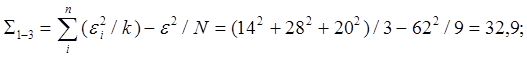
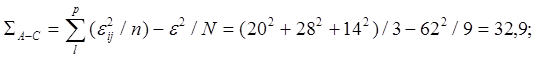
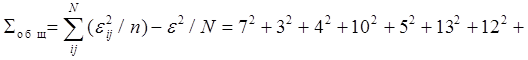
Сумма квадратов погрешности воспроизводимости:

Находим число степеней свободы для групп факторов:

Находим дисперсии влияния групп факторов и воспроизводимости:

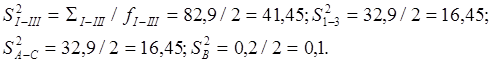
Оцениваем значимость влияния групп факторов по критерию Фишера:

F_{расч I-III} =  F_{расч 1-3} = 16,45/0,1=164,5

F_{расч A-C} = 164,5; F_табл = 19,2 (при P = 95 % и  = 2).

Поскольку F_табл < F_расч , влияние всех групп факторов (с вероятностью 95%) значимо.

Находим коэффициенты дисперсионной модели по формулам:

  ;      .

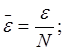
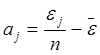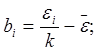
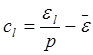Модель в качественной форме выглядит так:

Параметры модели:

= =;  =;

=;

;  =;          =;

=;  =;

=;

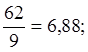
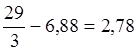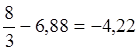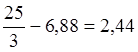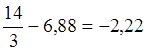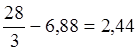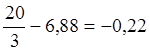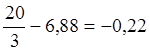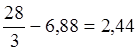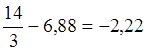= =0,31;  (для P=95%).

Модель

или

.

Лучшее сочетание факторов (факторы I,2,B) по извлечению

С целью закрепления материала рекомендуется самостоятельно:

1. Рассчитать дисперсионную модель не только для извлечения но и содержания золота в концентрате  b.

2. По полученным моделям для  и b  рассчитать результаты для   в с е х   возможных вариантов сочетаний факторов, представив данные в виде табл.4.13,

Прогноз результатов обогащения по  модели     Табл. 4.13 

Номер опыта	Факторы	, %	b , г/т
1	I   1   A	86,22 ± 1,3
2	I   1   B	88,88 ± 1,3
...	...  ...  ...	...	...

а также в виде графика в координатах  =.

3. Нанести на графике поля корреляции режимов кривую обогатимости _max  = (для этого надо соединить верхние точки корреляционного поля плавной линией).

4. Рассчитать по полученной модели условия, обеспечивающие: а) получение максимального извлечения золота в концентрат;  б) получение концентрата наилучшего качества; в) получение концентрата заданного качества ( = 107 г/т).

Контрольные вопросы.

1. В чем заключаются методические особенности дисперсионного анализа?

2. Составьте матрицу планирования по схеме латинского квадрата для трех групп факторов при четырех уровнях.

3. Какую информацию можно получить из дисперсионной модели 

5.  АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

5.1.  Оформление результатов научного исследования

4.1.1.  составление первичной документации

Непосредственно перед началом исследования составляется первичная документация, куда входят рабочий журнал наблюдений для внесения данных о режиме опытного технологического процесса, дата и время проведения опыта, замечания по визуальному наблюдению, число опытов и другие параметры. Кроме рабочего журнала наблюдений необходимо иметь журналы сдачи проб, направляемых для обработки и производства химических, минералогических и других анализов.