Математика \ Математическое моделирование

Математическое планирование экспериментов. Планирование экстремальных экспериментов. Объект исследования, критерий оптимизации и факторы, страница 10

Следовательно, получим модели

e = 64,9 - 0,62 х1 + 1,38 х2 + 0,12 х3 - 5,4 х4 ;

b = 10,25 + 0,25 х1 - 0,25 х2 - 2,75 х3 + 3,25 х4 .

Определим средние погрешности воспроизводимости для средних результатов, пользуясь формулой для двух параллельных опытов:

 = 1,58;

 = 0,94.

Погрешности коэффициентов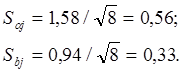

Предельное значение коэффициентов при 

и

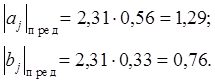
Отбросив незначимые коэффициенты, получим модели

e = 64,9 + 1,38 х2 - 5,4 х4 ;

b = 10,25 - 2,75 х3 - 3,25 х4.

Конечно, модели получились информационно бедными, так как потеряно по два коэффициента каждой модели.

Проверку на адекватность выполнять не будем (предоставив это выполнять студентам самостоятельно), а проведем интерпретацию моделей.

Извлечение зависит в основном от длины участка  а  стола, с которого производится съем концентрата (извлечение тем больше, чем больше этот участок), и угла наклона стола (извлечение тем больше, чем меньше угол наклона). Это соответствует нашим представлениям о процессе. Несколько неожиданным оказалось отсутствие влияния расхода воды на извлечение. Видимо, подается избыточное количество воды.

Качество концентрата предопределяется величиной участка стола b , причем чем меньше этот участок, тем лучше. Следует помнить, что этот вывод справедлив только в диапазоне изменения факторов, принятых в эксперименте.

Качество зависит и от угла наклона стола. Чем больше угол, тем выше качество. Это тоже соответствует естественному ходу вещей.

Найдем оптимальное решение в области экспериментирования при условии e ® ; b = 10 г/т. Оптимизацию выполним графическим методом (рис.4.2).

Поскольку модели не полны, возможности оптимизации ограничены. Наносим точку 1 с координатами e = 64,9 % и b = 10,25 г/т с режимом (0; 0; 0; 0).

Придаем фактору х2 приращение  +1, получаем точку   с режимом (0; +1; 0; 0), затем фактору   х4    даем приращение -1, получим точку    с режимом (0; +1; 0; -1), так как фактор х3 не входит в уравнение для извлечения, придаем ему такое приращение, которое приближает нас к ограничению (это приращение -1), получаем точку    с режимом (0; +1; -1; -1).


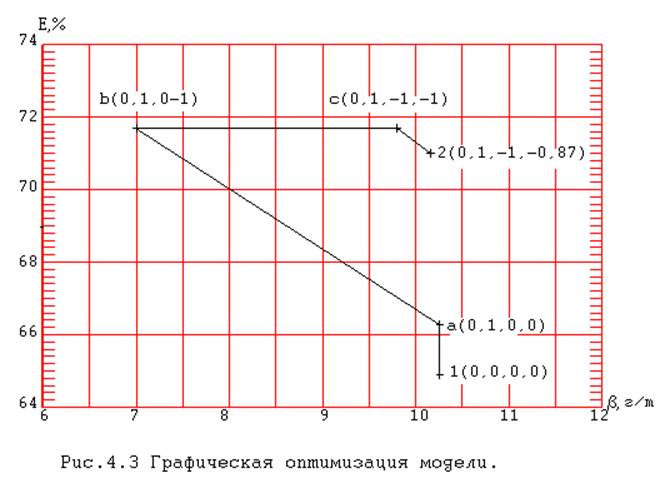Из точки  пойдем к ограничению по переменной  х4 , увеличивая ее, и  придем в точку 2, которая есть решение. Определить долю увеличения  х4 можно, взяв соотношение отрезков 2/=0,13. Следовательно, в точке 2 значение фактора   х4   равно – 1 + 0,13 = - 0,87.

Решением задачи является режим   х1 = 0;  х2 = +1;  х3 = -1; х4 = -0,87. При этом достигается e = 71,1% и b = 10 кг/т. Режим в натуральных единицах:  х1 = 20 л/мин,  х2 = 35 см,  х3 = 15 см,  х4  = 58,260.

Вопросы для самоконтроля.

1.Что такое матрица планирования эксперимента?

3.  В чем различие полного и  дробного факторного экспериментов?

4.  Каков физический смысл коэффициентов в регрессионной модели, получаемой методами математического планирования эксперимента?

4.1.9. Проведение эксперимента

Построив план приступают к подготовке эксперимента. При проведении эксперимента в какой - либо точке плана реализуют несколько параллельных опытов (Табл.4.8). При этом не удается получить соответствующих результатов, поскольку всегда присутствует ошибка опыта. Ошибка опыта является суммарной величиной и состоит из ошибок измерения факторов, параметра оптимизации и ошибок при проведении опыта.

Ошибку опыта в планировании эксперимента называют ошибкой воспроизводимости. Знание ошибки воспроизводимости необходимо для анализа данных эксперимента. Воспроизводимость обычно оценивают по результатам параллельных опытов, проведенных на основных уровнях, либо в какой либо точке плана или путем повторения каждого опыта плана (Табл. 4.9).

Реализация плана эксперимента                      ® j                           Табл. 4.9

Скачать файл