Математическое планирование экспериментов. Планирование экстремальных экспериментов. Объект исследования, критерий оптимизации и факторы, страница 13

В сложных условиях, особенно при низкой точности измерений, целесообразно применять специальные планы, которые отличаются указанным достоинством: не требуют вычисления характеристик гиперповерхности и, - в то же время, - могут привести к оптимуму.

          Специальные планы необходимы для того, чтобы гарантировать

испытание возможности движения по всем возможным направлениям.

          К таким (адаптационным) методам оптимизации относится

симплекс метод.

Суть симплекс метода заключается в том, что в  - мерном

пространстве строится правильный многогранник, вершины которого соответствуют условиям выполнения опытов.

Координаты вершин и образуют собственно план симплекс метода..

Если выбран основной уровень факторов  и интервал варьирования   и исследуются   факторов, то необходимо поставить в начале +1  опытов.

Значения факторов в каждом опыте определяются по формуле

 ,                                                     (4.15)

причем     определяются в соответствии с табл.4.11

Коэффициенты для выбора координат симплекса. Табл.4.11

Номер опыта	Ф    а    к    т    о    р    ы
				…
1				…
2				…
3	0			…
4	0	0		…
. . .	. . .	. . .	. . .	…	. . .
	0	0	0	0

Если, например, необходимо составить симплекс план для двух факторов, то вначале ставят три опыта со следующими координатами:

1-й опыт

;

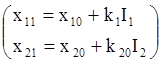2-й опыт

;

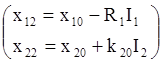3-й опыт

.

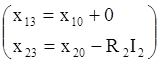Величины     и    определяются по формулам

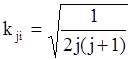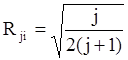;               , где   -   порядковый номер фактора.

Так, если х₁₀ = 0 и х₂₀ = 0, а I₁ = I₂ = 1, то координаты опытов будут (0,5; 0,289); (-0,5; 0,289) и (0; -0,577).

Алгоритм движения к оптимуму с помощью симплекс метода таков.

1.Поставить опыты в вершинах симплекса.

2.Выбрать из результатов самый плохой.

3.Заменить условия осуществления самого плохого опыта новыми, соответствующими “переворачиванию” симплекса. Предполагается, что если заменить условия плохого опыта противоположными, могут быть получены лучшие результаты.

Координаты новой вершины находят по формуле

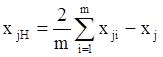_з  при j¹p,            

где m-число факторов; х_jз- значение j-го фактора в заменяемой вершине (опыте); х_iн-значение i-го фактора в новой вершине; р – номер меняемого опыта.

Подчеркнем еще раз, что в сумму 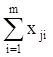 значение x_j для заменяемого опыта не входит.

4. Замена условий и постановка новых опытов осуществляется до тех пор, пока значение хотя бы одной координаты х систематически изменяется в одном направлении. Как только значение x_j начнут колебаться около некоторого уровня (симплекс «закручивается»), то поиск заканчивается.

Если после замены худшего опыта вновь получают худший результат, заменяют условия следующего плохого опыта и т.д.

ПРИМЕР 3

С целью более детального изучения методов оптимизации введем понятие условного объекта, задаваемого уравнением

y=f(x₁, x₂,…,x_n).                                        (4.16)

Экспериментатору это уравнение неизвестно. Значения у получают в результате опыта. В примере же будем получать результаты «опыта» путем расчетов по уравнению (4.16).

          Пусть объект обладает свойствами, соответствующими уравнению

y = 4 + 12х₁ - х₁² + 30х₂ - 3х₂².                   

Найдем экстремум функции симплекс методом. Выберем основной уровень факторов. Предположим, что экстремум находится вблизи значений х₁₀ = 3 и х₂₀ = -1, которые и примем за основной уровень. Интервалы варьирования установим  I₁ = 1,0 и I₂ = 1,5.

Тогда

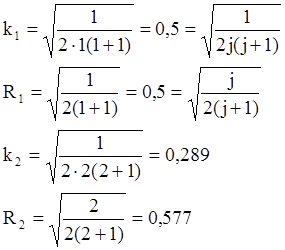
Находим координаты первых трех опытов,  для вершины 1

m+1=2+1=3;

x₁₁=3+0,5×1,0=3,5;

x₂₁=-1+0,289×1,5=-0,565;

для вершины 2

х₁₂=3-0,5×1,0=2,5;