Математическое планирование экспериментов. Планирование экстремальных экспериментов. Объект исследования, критерий оптимизации и факторы, страница 14

х₂₂=-1+0,289×1,5=-0,565;

для вершины 3

х₁₃=3+0=3,0

х₂₃=-1-0,577×1,5 = -1,865.

Получены следующие результаты опытов (в примере мы их получаем, подставляя координаты вершин в исходное уравнение):

у₁=15,84; у₂=9,89; у₃=-35,5.

Самый худший результат у₃=-35,5. Следовательно, условия опыта 3 необходимо заменить. Геометрическая траектория движения к оптимуму представлена на рисунке 4.4.

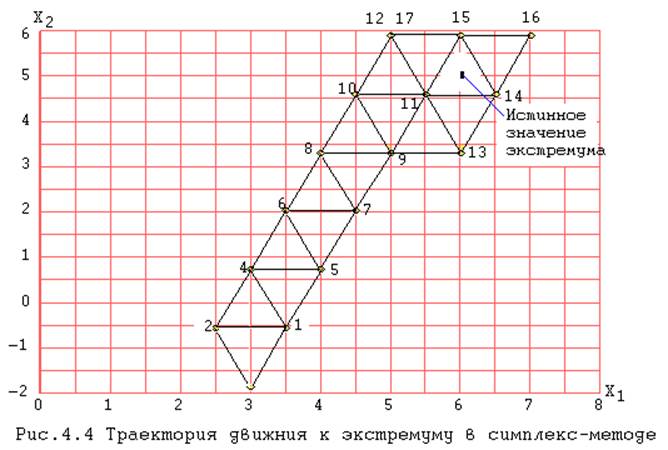Вычисляем координаты вершины 4.

х₁₁=3,5;

х₂₁=-0,565(15,84);

х₁₂=2,5;

х₂₂=-0,565(9,89);

х₁₄=3,0;

х₂₄=0,735(52,1).

Подставим эти координаты в уравнение (2):

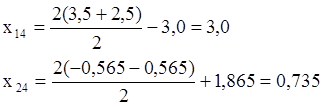
Результат:   у=52,1.

Сравнивая результаты у₁; у₂; у₄, видим что худший у₂. Вычисляем координаты вершины 5 и у₅:

х₁₁=3,5;

х₂₁=-0,565(15,84);

х₁₄=3,0;

х₂₄=0,735(52,1);

х₁₅=4,0;

у₁₅=0,735(57,1);

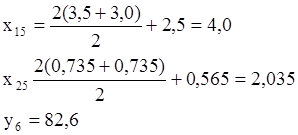
Далее (выполнить самостоятельно) получаем вершины с координатами: вершина 7 (4,5; 2,035); вершина 8 (4,0; 3,3); вершина 9 (5,0; 3,3); вершина 10 (4,5; 4,6); вершина 11 (5,5; 4,6). Результаты: у₉=105; у₁₀=113; у₁₁=112,32.

Находим координаты вершины 12

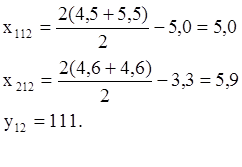
Видим, что координаты вершины 12 соответствуют худшим результатам, чем оставшиеся 10 и 11. Поэтому возвращаемся к предыдущему симплексу с вершинами 9, 10, 11 и выбираем худший результат, не обращая внимание на опыт 9. Следовательно, заменить необходимо вершину 10:

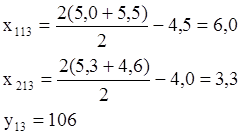
В этом новом симплексе координаты вершины 9 (5,0; 3,3); вершины 11 (5,5; 4,6); вершины 13 (6,0; 3,3). Худший результат у опыта 9.

Заменяем вершину 9:

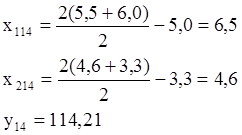
Результаты опытов 11, 13, 14:

у₁₁=112,32;

у₁₃=106;

у₁₄=114,21.

Заменяем вершину 13:

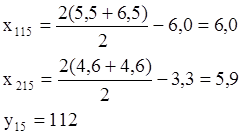
Получен худший результат, чем в опытах 11 и 14, поэтому заменяем опыт11:

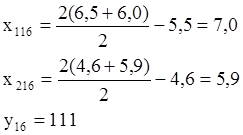
Это также худший результат, поэтому в симплексе 11, 14, 15 заменяем опыт 14:

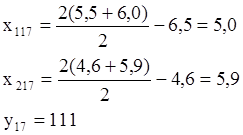
Вершины 17 и 12 совпадают, у₁₇=у₁₂=111. Снова получили худший результат. Итак, замена любой вершины симплекса 11, 14, 15 дает худшие результаты. Следовательно, экстремум находится внутри этого симплекса.

Далее можно уменьшить интервал варьирования и от любой вершины двигаться вновь. Если же с точностью до шага варьирования результаты не устраивают, можно считать задачу решенной.

Следовательно, координаты экстремума х₁»6,5; х₂»4,6; у=114,21. Истинные координаты экстремума х₁=6,0; х₂=5,0; у=115.

4.2. Дисперсионный анализ

          Дисперсионный анализ - раздел математики, проводящий

статистическое выявление влияния отдельных факторов  на результат эксперимента. Дисперсионный анализ (ДА) имеет дело главным образом с количественными факторами. Особенностью таких факторов является то, что они являются дискретными величинами, их уровням не соответствует числовая шкала и порядок уровней не играет роли.

Первоначально ДА был предложен английским статистиком Робертом Фишером (1925 г.) для обработки результатов агрономических опытов. Дисперсионный анализ относится к числу активных методов экспериментирования.

Дисперсионные планы можно считать многоуровневыми дробными факторными планами, отличающимися установивщейся традицией исследования влияния изменения качественных факторов и использования для выводов оценки значимости различия дисперсий и традиционным отсутствием записи модели в явной форме.

В связи со специфичностью (многоуровневостью) планов и качественным определением аргументов для дисперсионного анализа развит специфический аппарат обработки результатов.

При дисперсионном анализе используются однофакторные и многофакторные планы, последние из которых разделяют на блочные, латинские квадраты, греколатинские квадраты и т.д.

          Обработка результатов всегда ведется по одной и той же схеме

(меняется только число определяемых величин с изменением размера плана).

ПРИМЕР 4

Приведем схему дисперсионного анализа на следующем примере: выбрать с помощью схемы дисперсионного анализа наилучшую конструкцию импеллера флотационной машины, тип собирателя и тип вспенивателя для флотации золотоносной руды. Оценку вести по извлечению золота в концентрат и содержанию его в концентрате.

Используем латинский квадрат (табл.4.12).

Т а б л и ц а 4.12

Схема латинского квадрата