Математическое планирование экспериментов. Планирование экстремальных экспериментов. Объект исследования, критерий оптимизации и факторы, страница 5

k – номер опыта,

K – число опытов.

2) Нормированность: сумма квадратов элементов каждого столбца равна числу опытов

S (x_ik)² = K                                                 (4.5)

Это свойство является следствием того, что кодированные значения факторов в матрице задаются  ± 1.

3)Ортогональность: сумма почленных произведений любых двух вектор-столбцов матрицы равна нулю:

S x_ik×x_ik = 0                                             (4.5)

4)Ротатабельность: точки в матрице планирования выбраны таким образом, что точность предсказания значений критерия оптимизации одинакова на равных расстояниях от центра эксперимента.

Благодаря этим свойствам сильно упрощается обработка результатов методами регрессионного анализа.

4.1.7. Нахождение оценок коэффициентов в уравнении регрессии

Рассмотрим ПФЭ 2ⁿ . Основная задача планирования – это нахождение по результатам эксперимента неизвестных коэффициентов модели.

Рассмотрим аппроксимацию функции отклика с помощью линейной модели

Y = S b_j x_j ,                                                             (4.6)

где b_j  - выборочные оценки коэффициентов модели.

Для нахождения коэффициентов уравнения регрессии (4.6) применим метод наименьших квадратов (МНК). Для этого рассмотрим функцию

F(b₀, b₁, …, b_n) = S (Y_i - Sb_j×x_ij)²                                    (4.7)

характеризующую сумму квадратов отклонений опытных точек Y_j от величин, предсказанных регрессионным уравнением (4.6).

Коэффициенты b_j (где j = 0,1,2, …, m) находим из условия min F(b_0, b₁, …, b_m). Оно сводится к построению системы уравнений при j = 0,1,2, …, k

¶ F/¶ b_j = 0                                                (4.8)

Запишем систему (4.8), учитывая функцию (4.7):

b₀  Si  +  b₁Sx_i1 +  b₂Sx_i2 + …    + b_mSx_im  =     S Y_i ;

b₀Sx_i1 + b₁Sx_i1² + b₂Sx_i1x_i2 + … + b_mSx_i1x_im = SY_ix_i1;

………………………………………………………

b₀Sx_im + b₁Sx_i1x_im + b₂Sx_i2x_im + … + b_mSx_i1x_im² = SY_ix_im.

Учитывая условие ортогональности (4.5), легко вычислить коэффициенты регрессии при  j = 1,2, …, m :

b_j  = (S x_ij Y_i) /n ; b₀ = (S Y_i) /n                     (4.9)

Точность и надежность вычисленных коэффициентов зависят от свойств выборки и нуждаются в статистической проверке.

Величина коэффициентов b_j  указывает на силу влияния факторов: чем больше значение коэффициента, тем сильнее влияет фактор.

ПРИМЕР 1

Оптимизация модели методом полного   факторного эксперимента                                      

(ПФЭ) на примере грохота.

Допустим, оптимизируемой функцией является эффективность грохочения 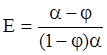                  , где  a и j содержание минусового класса соответственно в питании и в подрешетном продукте.

В качестве факторов примем: х₁ - угол наклона грохота, град; х₂-расход воды на грохочение, м³/мин; х₃ - частота пульсации, с^-1. 

Предполагаемые наилучшие значения- нулевой режим: х₁₀=20°; х₂₀=1 м³/мин; х₃₀=2 с^-1.

Выбраны следующие интервалы варьирования: Dх₁=3°; Dх₂=0,2 м³/мин; Dх₃=0,4 с^-1.

Интервалы варьирования приняты из следующих соображений: изменение хода процесса заметно, но в то же время процесс сильно не нарушается. Таким образом, уровни +1 и –1 соответствуют следующим значениям факторов:

+1                                        -1

х_1max=23°                             х_1min=17°

x_2max=1,2 м³/мин                 х_2min=0,8 м³/мин х_3max=2,4 с^-1                         х_3min=1,6 с^-1

Составим план ПФЭ (см. таблицу).

План ПФЭ 2³ и результаты опытов и расчетов