Рыночная система: спрос и предложение. Основные понятия и формулы. Параметры рыночного равновесия, страница 6

Задача 3. Дано: производственная функция ,  где L - труд, К - капитал. Общие  издержки  равны 36 маркам,    - цена труда, = 9 - цена капитала. Определите: 1) какое количество экономических ресурсов купит фирма для максимизации совокупного продукта; 2) максимальное значение совокупного продукта. Полученные решения проиллюстрируйте графически.

Задача 4. Дано:  а),   б) ,   в) ,   г) TР = 2L + 4K.  Определите:  1) E_TP  (для всех производственных функций);  2)    (для функций “а” и “б”);   3) TР, если: а) L = 1,  К = 2; б) L = 8,  К = 16 (для всех производственных функций). Прокомментируйте полученные результаты. Постройте графики изоквант для всех производственных функций, если TР = 10.

Задача 5.Дано: , , 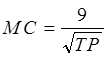TFC=56. Определите  получает ли фирма экономическую прибыль, а если да, то и ее значение, если фирма покупает по 16 единиц труда и капитала, а рыночная цена производимого товара равна 4 маркам?

Задача 6*.Господин Х для производства зубной пасты использует три экономических ресурса: Т - земля,  L - труд,  К - капитал.  , , = 80, . Определите минимальную величину общих издержек на покупку ресурсов, если господин Х планирует произвести 120 условных единиц зубной пасты.

Задача 7.Дано: , , = 1,  , TC = 36. Определите: 1) какое количество экономических ресурсов купит фирма для максимизации совокупного продукта; 2) максимальное значение совокупного продукта.

Задача 8*.Докажите: 1) если  AC = MC, то AC минимальные (AС_min); 2) если  AVC = MC, то  AVC  минимальные (AVC_min).

Задача 9*.Дано: производственная функция , где L - труд, К - капитал. Общие постоянные издержки равны 750 маркам. , = 4, . Определите: 1) какое количество единиц труда и капитала будет покупаться фирмой, если ТР = 100; 2) значения  MC и  AVC, если  TP = 100.

Задача 10**.Дано: производственная функция , где L - труд, К - капитал. Общие постоянные издержки равны 192 маркам. , = 16, . Определите: 1) какое количество единиц труда и капитала будет покупаться фирмой, если TР= 6; 2) значение прибыли, если  TP =  6, а рыночная цена выпускаемого товара равна 100 маркам; 3) значения   MC, AC  и  AVC, если  TP = 6; 4) значение  TP, при котором  AC достигают минимума; 5) значение  TP, при котором  AVC достигают минимума.

Тема 4. Фирма в условиях совершенной конкуренции

Основные понятия и формулы

1) TR = Q · P,  AR = TR / Q, 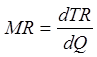  .  = . В условиях совершенной конкуренции для фирмы  MR =Р, т.к.  , а в условиях несовершенной конкуренции  MR < Р , т.к. < 0.

2) Правило максимизации совокупной прибыли фирмы.

PR = TR - TC (TR  > TC). Найдем dPR / dQ = 0.  dPR / dQ = dTR / dQ - dTC / dQ = 0, когда  MR = MC. Таким образом, для максимизации совокупной прибыли фирмы в условиях совершенной конкуренции (SR) необходимо производить такой объем продукции Q, при котором  MR = MC (P = MC) и P > AC. Если P = MC  и  P = AC, то PR = 0.

3) Правило минимизации совокупных убытков фирмы.

-PR = TR - TC (TVC <  TR  <  TC). Найдем d (-PR) / dQ = 0, получим MR = MC. Таким образом, для минимизации убытков фирмы в условиях совершенной конкуренции (SR) необходимо  производить  такой объем  продукции Q,  при котором   MR =  MC (P = MC) и AVC <  P < AC.

4) Если  TR = TVC   (P = AVC), то фирма должна принять решение о дальнейшей целесообразности продолжения производства. Если  TR < TVC   (P <  AVC), то фирма ничего не производит (Q = 0).

5) Правило равновесия конкурентной фирмы в долгосрочном периоде (LR).

Фирма производит такой объем продукции Q, при котором MR = P = MC = AC_min .

Пример. Дано: TC=Q³ - 2Q² + 8Q + 100, где Q - объем выпуска товара. Определите  в условиях совершенной конкуренции (SR):

1) значение максимальной совокупной прибыли фирмы если рыночная цена товара равна 63 маркам.

Решение. Найдем МС.  MC= dTC/ dQ = 3Q² - 4Q +8. MC= Р, откудаQ = 5. Определим AC при Q = 5.  AC =TC/Q=Q²  - 2Q+ 8+100 / Q,  подставив Q = 5, получим АС = 43. Тогда  Pr =(P -AC)Q. Таким образом, Pr = 100;