CS =  - TE, где TE = Pi × Q.
- TE, где TE = Pi × Q.
3) Правило максимизации совокупной полезности или условие равновесия потребителя.
Если дана функция совокупной полезности TU = f (Q1,
Q2, ..., Qn) и уравнение дохода I = = P1
Q1 + P2 Q2 + ... + Pn
Qn, то TU
достигает максимума, когда выполняется условие  или
если MRS12 = Р1 /Р2 ; MRS13 = Р1 / Р3 ; ... ; MRS1n = = Р1 /
Рn.
или
если MRS12 = Р1 /Р2 ; MRS13 = Р1 / Р3 ; ... ; MRS1n = = Р1 /
Рn.
4) DAS = A (![]() , I 1) - A (PA
, I ) - эффект замещения, где DAS - изменение количества товара A вследствие
эффекта замещения; A (
, I 1) - A (PA
, I ) - эффект замещения, где DAS - изменение количества товара A вследствие
эффекта замещения; A (![]() , I 1) - потребление товара
A при новой цене
, I 1) - потребление товара
A при новой цене ![]() и новом доходе I 1; A
(PA , I ) - потребление товара A при
старой цене PA и старом доходе I. DAI = A (
и новом доходе I 1; A
(PA , I ) - потребление товара A при
старой цене PA и старом доходе I. DAI = A (![]() , I ) - A (
, I ) - A ( ![]() ,
I 1 ) - эффект дохода, где DAI - изменение количества товара A вследствие
эффекта дохода; A (
,
I 1 ) - эффект дохода, где DAI - изменение количества товара A вследствие
эффекта дохода; A ( ![]() , I ) - потребление товара A при
новой цене
, I ) - потребление товара A при
новой цене ![]() и старом доходе I. DAT = DAS + DAI - общее изменение потребления товара A
вследствие изменения его цены.
и старом доходе I. DAT = DAS + DAI - общее изменение потребления товара A
вследствие изменения его цены.
5) Товар A - нормальный (полноценный) товар, если при увеличении (снижении) его цены: DAS < 0, DAI < 0 и DAT < 0 ( DAS > 0, DAI > 0 и DAT > 0 ).
Товар A - низкокачественный (малоценный) товар, если при увеличении (снижении) его цены: DAS < 0, DAI > 0, | DAS | > | DAI | и DAT < 0 ( DAS > 0, DAI < 0, | DAS | > | DAI | и DAT > 0 ).
Товар A - товар Гиффена, если при увеличении (снижении) его цены: DAS < 0, DAI > 0, | DAS | < | DAI | и DAT > 0 ( DAS > 0, DAI < 0, | DAS | < | DAI | и DAT < 0 ).
Пример. Дано: функция предельной полезности товара А MUA =10 - QA, функция совокупной полезности товара BTUB = 18QB - 1,5QB 2, PA = 3, PB = 6. Господин Х собирается потратить на покупку товаров 24 марки. Определите:
1) какое количество каждого товара он купит?
Решение. Используем правило максимизации совокупной полезности  .
Найдем
.
Найдем  ,
тогда имеем систему:
,
тогда имеем систему: 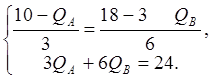 Решая ее, получаем QA
= 4, QB=
2;
Решая ее, получаем QA
= 4, QB=
2;
2) значение потребительского излишка, если PA = 3, предельная полезность денег постоянна и равна 2, а господин Х купил: а) 6 единиц товара А; б) 4 единицы товара A.
Решение. а)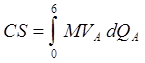 -
3×6. Найдем MVA. MVA
= (10 - QA )/2. Tогда CS = 3. б)
-
3×6. Найдем MVA. MVA
= (10 - QA )/2. Tогда CS = 3. б) 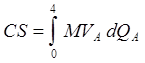 - 3×4. Tогда CS = 4. Очевидно,
что при покупке оптимального количества товара A потребительский излишек
максимальный.
- 3×4. Tогда CS = 4. Очевидно,
что при покупке оптимального количества товара A потребительский излишек
максимальный.
Задача 1. Проверьте, правильно ли поступил господин Х, купив 2
единицы товара А и 4,5 единицы товара В, если известно, что![]()
![]() ,
PA = 2, PB = 4, I = 22. Если неправильно, то какое количество товаров
он должен был купить?
,
PA = 2, PB = 4, I = 22. Если неправильно, то какое количество товаров
он должен был купить?
Задача 2. Используя данные таблицы, определите оптимальное количество покупаемого товара и потребительский излишек для каждого количества товара, если рыночная цена товара равна 6 маркам.
|
Количество товара, кг |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Предельная ценность, марка |
20 |
18 |
11 |
7 |
5 |
2 |
1 |
Задача 3. Дано: функция предельной ценности сахара MV=5 - Q. Определите значение максимально возможного потребительского излишка, если рыночная цена килограмма сахара равна одной марке. Полученное решение проиллюстрируйте графически.
Задача 4. Дано: ![]() ,
, ![]() I = 72. Определите, какое количество
товара А приобретет господин Х для максимизации удовлетворения своих
потребностей и сколько денег он предпочтет сберечь?
I = 72. Определите, какое количество
товара А приобретет господин Х для максимизации удовлетворения своих
потребностей и сколько денег он предпочтет сберечь?
Задача 5*. Дано:![]() , PA = 4, PB = 9, величина дохода потребителя равна 36 маркам.
Определите: 1) максимальное значение совокупной полезности; 2) MUM
в состоянии равновесия потребителя; 3) эффект замещения и эффект дохода для
товара А, если его цена уменьшилась в 4 раза. Полученные решения
проиллюстрируйте графически.
, PA = 4, PB = 9, величина дохода потребителя равна 36 маркам.
Определите: 1) максимальное значение совокупной полезности; 2) MUM
в состоянии равновесия потребителя; 3) эффект замещения и эффект дохода для
товара А, если его цена уменьшилась в 4 раза. Полученные решения
проиллюстрируйте графически.
Задача 6*. Используя данные таблицы, определите: 1) количество единиц товаров A, B, C, D, которое приобретет господин Х для максимизации совокупной полезности от их потребления, если цены товаров соответственно составят 18, 6, 4, 24 марки, а его доход равен 106 маркам; 2) количество сберегаемых марок; 3) максимальное значение совокупной полезности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.