Исследование особенностей различных видов промежуточных рельсовых скреплений с корректировкой нормативов их технического обслуживания (Отчет о научно-исследовательской работе), страница 8

2. геометрические и конструктивные параметры верхнего строения пути, поддающиеся анализу неоднородности;

3. квантификация неоднородности эти параметров.

Исследования верхнего строения пути различными средствами контроля показывают, что даже на линиях с наилучшим (близким к идеальному) состоянием пути существует разброс комплексных показателей, несмотря на одинаковые конструкцию и нагрузку.

Именно по этим критериям и был произведен анализ состояния пути.

Различие в состоянии верхнего строения пути – явление весьма неблагоприятное из технических и экономических соображений. Оно проявляется в виде местных ухудшений плавности движения поездов и неравномерности изнашивания верхнего строения пути.

Раньше текущие ремонты пути, выполнявшиеся вручную, допускали изначально наличие неоднородности характеристик пути. Сейчас же, при использовании в работе путевых машин, это сведено к минимуму. О необходимости ремонта свидетельствует превышение допускаемых отклонений.

Можно считать, что неоднородность характеристик верхнего строения пути превращается в одну из обоснованных причин больших разбросов его долговечности.

5.1. Определение геометрической неоднородности пути

Среди геометрических величин для определения геометрической неоднородности, учитывая простоту измерений и рациональное отображение состояния верхнего строения пути в целом и промежуточных рельсовых скреплений в частности, наиболее пригодны ширина колеи, возвышение рельсовых нитей, подуклонка рельсов.

Эксперименты показали, что для анализа неоднородности характеристик верхнего строения пути целесообразным интервалом при считывании ширины колеи, возвышения и подуклонки рельсов при непосредственном измерении является расстояние 5 м.

5.2. Обработка результатов эксперимента и построение гистограмм

Группа объектов, объединенных по некоторому качественному или количественному признаку называется статистической совокупностью.

Совокупность однородных показаний, объединенных по общему признаку, принято называть генеральной.

Для того чтобы выборка была репрезентативной, необходимы два условия:

1. в выборке должно быть достаточное число измерений;

2. измерения должны отражать генеральную совокупность, т.е. обладать характеристиками присущими генеральной совокупности.

С увеличением числа наблюдений (объема выборки) характеристики выборочной совокупности (среднее значение признака, его дисперсия и др.) приближаются к характеристикам генеральной совокупности.

Объем выборки можно определить пользуясь таблицей достаточно больших чисел. Для этого зададимся величиной вероятности р = 0,95 (обычно принимается при научных исследованиях), выражающей степень надежности (репрезентативности) выборки, и назначим допустимую ошибку е = 0,1, то достаточно большое число наблюдений (объем выборки) должен быть не менее 96 измерений.

После проведения экспериментальных измерений различных характеристик пути нами были получены простые статистические совокупности (прилож. 1.).

Для того чтобы установить закономерность измеряемой величины и ее характеристики, простая статистическая совокупность подвергается обработке, которая заключается в следующем.

1. Все данные располагаются в порядке возрастания или убывания значений случайной величины. Получается, так называемый, вариационный ряд, а его объекты - варианты.

2. Данные вариационного ряда разбиваются на группы (разряды). Число разрядов зависит от объема выборки. Практика показывает, что в большинстве случаев целесообразно выбирать число разрядов порядка 10…20. Величина интервала разряда зависит от размаха колебаний измеряемой величины и минимальных интервала, возможных по различным ограничениям.

Величина интервала С определяется по формуле

где  – соответственно максимальное и минимальное значение измеряемой величины Х;

К – число разрядов.

Значения измеряемой величины, совпадающее с границами интервалов, можно условно отнести (для всех разрядов) к первым (в порядке расположения) или вторым разрядам.

По вариационному ряду в каждом разряде подсчитывается число измерений (частоты), а затем определяется значение частостей:

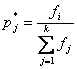
где   – частость, выражающая статистическую вероятность того, что измеряемая величина окажется в j- ом разряде;

f_i – число наблюдений в j- ом разряде;

j – номер разряда;

К – число разрядов.

Полученные значения разрядов, частот и частостей оформим в виде статистического ряда для простой статистической совокупности (табл. 1).

Таблица 1

Статистический ряд (ПЧ-11, круговая кривая)

Значения промежутков в разряде	Частота, fi	Частость,
1	2	3
1534-1537 1537-1540 1540-1543 1543-1546 1546-1549	2 12 27 0 1	0,047619 0,285714 0,642857 0,000000 0,023810
Итого	42	1,0000

По данным статистического ряда определяют числовые характеристики простой статистической совокупности:

Первый начальный момент, или статистическое среднее

где   –  среднее значение случайной величины в j-ом разряде статистического ряда.

Статистическая дисперсия

где  - статистический второй начальный момент

Статистическое среднее квадратическое отклонение

Вычисление числовых характеристик удобно производить в табличной форме (табл. 2).

Таблица 2

Числовые характеристики простой статистической совокупности

j
1	2	3	4	5	6
1 2 3 4 5	1534-1537 1537-1540 1540-1543 1543-1546 1546-1549	1535,5 1538,5 1541,5 1544,5 1547,5	0,047619 0,285714 0,642857 0,000000 0,023810	73,11904762 439,5714286 990,9642857 0,000000 36,8452381	112274,2976 676280,6429 1527571,446 0,000000 57018,00595
Итого			1,0000	1540,50000	2373144,393

Числовые характеристики рассматриваемой простой статистической совокупности будут следующими:

 мм