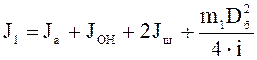,
(11.24)
где i – передаточное число механической передачи, i = 1
m1 – полумасса каната, кг
,
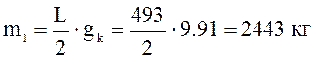
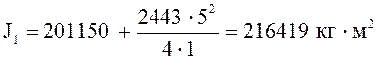
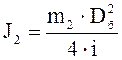(11.25)
где m2 – масса относимая к исполнимому органу, кг
,
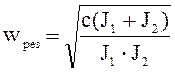(11.26)
где с – коэффициент жесткости
,
следовательно
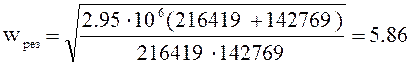с-1
11.24.3 Анализ показал, что резонансная частота входит в полосу пропускания системы (wср. > wрез.), а следовательно влияние упругостей на работу системы значительно и его следует учитывать. Т.е. необходимо построить такую систему управления, при которой возникшие механические колебания скорости исполнительного органа, вследствие упругого элемента, демпфировались электроприводом.
11.25 Силы внутреннего трения в тросе вызывают выделение энергии в окружающую среду, эта потеря энергии учитывается коэффициентом сопротивления b, который и учитывает коэффициент демпфирования.
 |
Рисунок 11.9 Структурная схема учета упругости каната
11.26 Для определения b, найдем передаточную функцию приведенной структурной схемы
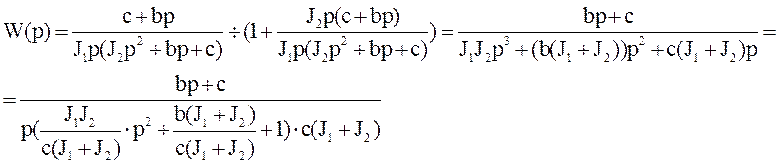
Если обратить внимание на первую
часть знаменателя полученного выражения, то его можно сравнить со знаменателем
колебательного звена второго порядка 
, т.е.
за счет приведенной структуры (11.9) в систему управления вводится
колебательное звено, которое и демпфирует, за счет электропривода, колебания
скорости исполнительного органа. Здесь Ту – постоянная времени
упругих колебаний двухмассовой системы, ξ – коэффициент демпфирования, который
определяет затухание колебаний. Очевидно
, 
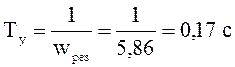Для определения коэффициента демпфирования воспользуемся диаграммой Вышнеградского (справочник /5/, стр. 94, рис. 2.18). Рекомендуемый участок выбора рабочей точки электропривода это заштрихованный участок, соответствующий ξ = 0,5 – 0,7, выберем, 0,7, следовательно
11.27 Вал двигателя и органа навивки каната опирается на подшипники скольжения, поэтому в структурной схеме следует также учесть коэффициенты вязкого трения а1 и а2, по диаграмме Вышнеградского они равны а1 = а1 = 2,41.
11.28 Вследствие наматывания троса момент сопротивления привода будет постоянно меняться, это видно и на расчетной диаграмме статического момента (рис. 8.2, б). При движении клети вверх с горизонта «-300» до приемной площадки момент сопротивления будет уменьшаться в зависимости от скорости, т.е.
 |
Схема 11.10 Учет изменения момента сопротивления
11.29 Использую возможности MATLAB6p5/Simulink, смоделируем схему, полученную в результате расчетов.
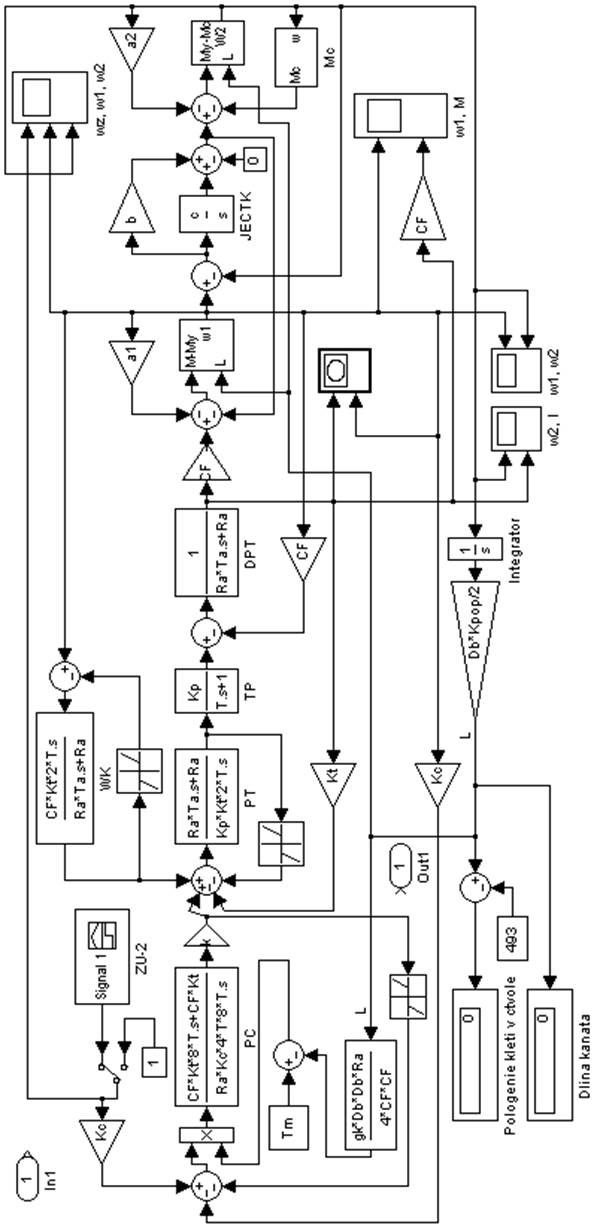
Схема 11.11 Динамическая модель MATLAB6p5/Simulink
12 ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ОДНОГО ЦИКЛА РАБОТЫ ЭЛЕКТРОПРИВОДА
При построении переходных процессов учтем все основные нелинейности, входящие в состав системы управления и заданной части электропривода (ограничение выходов регуляторов и силовых преобразователей, запаздывание в трогании двигателя, изменение момента сопротивления вследствие наматывания троса, вязкое трение в подшипниках, упругое действие троса и диссипацию).
12.1 Подадим на вход системы сигнал wзад., соответствующий подъему нагруженной клети с горизонта «-300» до приемной площадки. В итоге на выходе имеем скорость движения вала двигателя w1, клеть будет двигаться со скоростью V2, которой будет соответствовать угловая скорость w2.
wзад.
|
|
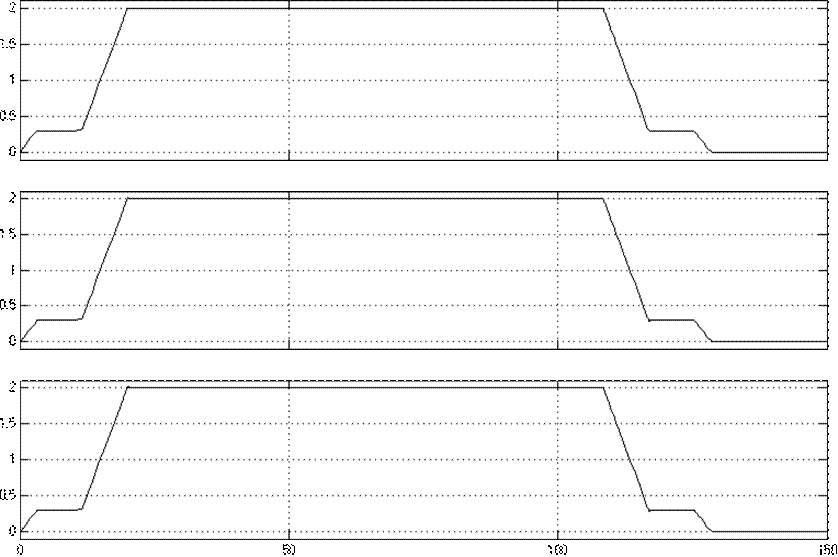
Рисунок 12.1 Графики скоростей задания, вращения вала двигателя, движения клети во времени
12.2 Представим также электромеханическую и механическую характеристики привода
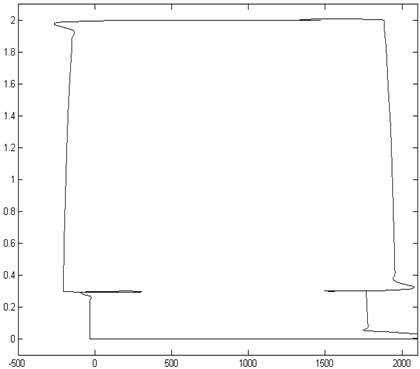
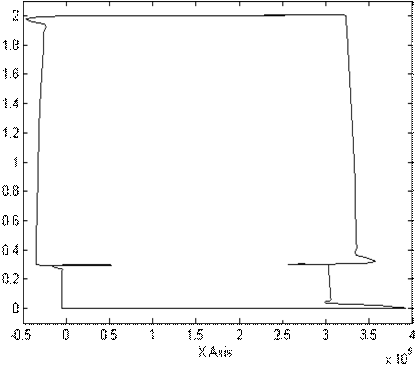
Рисунок 12.2
12.3 Покажем изменение тока и момента во времени, при этом на графике моментов приведем расчетную диаграмму (покажем жирной линией), построенную в пункте 8.3, д.
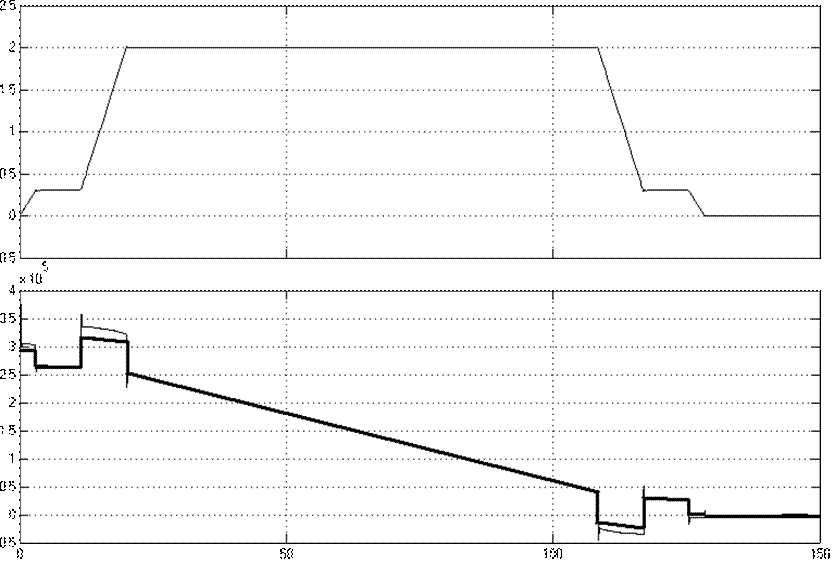
Рисунок 12.3 Тахограмма и диаграмма изменения момента во времени
Как видно из рисунка 12.3 диаграммы моментов почти полностью повторяют друг друга, лишь в моменты разгона и торможения значения моментов незначительно отличаются.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.