Транспорт как отрасль материального производства. Характеристика видов транспорта. Классификация автомобильных перевозок, страница 13

Для одного ТС за время в наряде количество перевезенных (планируемых) тонн (Q_Тн) груза и выполненных тонно-километров (Р_Тн)

QТн =Т н ⋅ lqегн+⋅γβс⋅⋅Vβт⋅⋅Vtтпр    и    РТн =Т н ⋅ qlнег⋅ γ+qβ⋅β⋅V⋅Vт т⋅t⋅прlег .

Для одного ТС за Д_к календарных дней эти показатели можно определить по следующим зависимостям:

QДк = Дк ⋅αв ⋅Тн ⋅ lqегн+⋅γβс⋅⋅Vβт⋅⋅Vtтпр    и    РДк = Дк ⋅ αв ⋅Тн ⋅ qнlег⋅ γ+qβ⋅β⋅V⋅тVт⋅ t⋅прlег .

Для парка ПС: за один день

QАи = Аи ⋅αв ⋅Т н ⋅ lqегн+⋅ γβс⋅⋅Vβт⋅⋅Vtтпр    и    РАи = Аи ⋅αв ⋅Т н ⋅ qlнег⋅ γ+qβ⋅β⋅V⋅Vт т⋅t⋅прlег , а за Д_к календарных дней

                                                         qн ⋅γс ⋅β⋅Vт                                                                       qн ⋅ γ q ⋅β⋅Vт ⋅lег

QАДи = АДи ⋅αв ⋅Тн ⋅ lег +β⋅Vт ⋅tпр    и    РАДи = АДи ⋅αв ⋅Т н ⋅ lег + β⋅Vт ⋅tпр                                                                                                        .

Полученные выражения используют для анализа, организации и планирования работы ПС.

4. Качественный и количественный анализ влияния техникоэксплуатационных показателей на производительность подвижного состава

4.1. Качественное влияние показателей на часовую производительность подвижного состава

Анализ влияния отдельных ТЭП на производительность ТС можно выполнить по следующей методике. Принимая в выражении один показатель за переменную величину при прочих постоянных, устанавливается характер зависимости производительности от этого показателя. Зависимости имеют либо ли^. x), либо дробно-линейный (W_x = a^x ⋅ x + b^x ) характер. Для нейный (W_x = a_x + b_x

x + c_x

конкретного ТЭП постоянные коэффициенты a_x, b_x и c_x могут быть величинами положительными, отрицательными или равными нулю. Графиком всякой дробно-линейной функции является равнобочная гипербола. Каждому значению постоянных коэффициентов (a_x; b_x; c_x) соответствует определенная кривая (прямая). Следовательно, зависимость производительности ТС от любого эксплуатационного фактора определяется семейством кривых, у которых различные значения a_x, b_x и c_x. Для выявления взаимосвязанных факторов на производительность используют метод определения относительных приращений. Относительное изменение результативной величины (A_x) рассчитывается по зависимости

∂W^x ⋅ x , A_x =

                                                                                                 ∂x   W_x

которое в математической статистике называют коэффициентом эластичности.

Рассмотрим влияние ТЭП на производительность ТС при простом цикле грузовых перевозок. Учитывая, что для этого случая γ_с = γ_q, то W_P = W_Q ^. l_ег. Следовательно, все показатели, кроме длины груженой ездки, на часовую производительность в тоннах (W_Q) и тонно-километрах (W_P) влияют одинаково.

Влияние грузоподъемности (q_н) и степени ее использования (γ) носит прямопропорциональный характер.

WQqн = bqн ⋅qн ;    WQγ = bγ ⋅ γ;    WQqнγ = bqнγ ⋅qнγ ;

н lег +γ⋅ββ⋅V⋅Vтт⋅tпр bγ = qн ⋅β ⋅Vт ;    bqнγ = β⋅Vт ; bq = ;    lег + β⋅Vт ⋅tпр lег +β⋅Vт

                                             н            ∂WQ      qн =     γ ⋅β⋅Vт        ⋅         qн                =1

                                         Aq = ∂qн ⋅WQ         lег + β⋅Vт ⋅tпр        qн ⋅ γ ⋅β⋅Vт           ,

lег +β ⋅Vт ⋅tпр

т.е.  Aq_н = Аγ = Аqγ = 1.   Это значит, что с увеличением фактической загрузки на 1 % производительность также возрастет на 1 %.

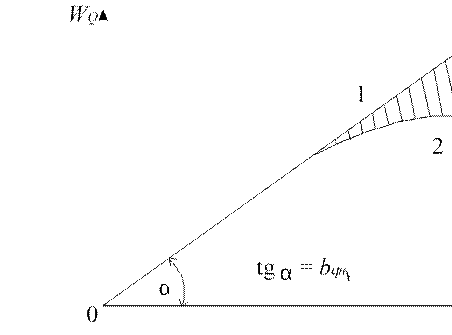
Рисунок 2

На практике увеличение грузоподъемности и степени ее использования может привести к снижению технической скорости ТС и увеличению времени простоя в пунктах погрузки и разгрузки, т.е. к отклонению от линейной зависимости, а при значительном росте qγ и даже к снижению производительности (кривая 2 на рис. 2).

Влияние коэффициента использования пробега на производительность носит дробно-линейный характер и изображается на графике равнобочной гиперболой.

β = βaβ+⋅cβ ;    aβ = qtнпр⋅γ ;

WQ

β