Выражение для полной амплитуды Е излучения, падающего под углом _____ и отраженного в направлении ______ будет иметь вид:
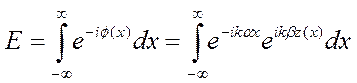
|
|
|
Рис. 3.11. Модель отражения лучей от криволинейной поверхности. |
Видно, что оно представляет собой Фурье-преобразование функции которую можно разложить в степенной ряд
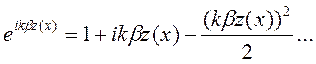 (3.48)
(3.48)
Таким образом, записать наше выражение для амплитуды поля рассеянного отражения можно в следующем виде:
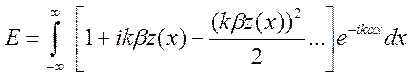 (3.49)
(3.49)
Первый член этого выражения является дельта-функцией при α = 0. Учитывая, что ______________________________ и, следовательно, _______________можно заключить, что этот член описывает спекулярную (зеркальную) составляющую рассеяния. Второй член можно переписать так:
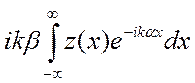
и мы видим, что он пропорционален преобразованию Фурье от функции высотной координаты z (x) поверхности. Вид этого выражения наводит на мысль, что удобнее вместо самой высотной функции использовать ее Фурье-преобразование a(q), где q — пространственная частота:
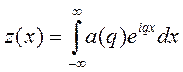
Таким образом, второй член уравнения (3.49) принимает вид:
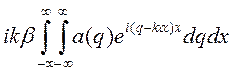
Пользуясь определением дельта-функции Дирака, которое мы рассматривали в п. 2.3, можно преобразовать последнее выражение к виду:
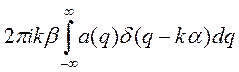 (3.50)
(3.50)
Это и есть искомый результат. Он говорит о том, что амплитуда излучения, отраженного в заданном параметром «направлении, пропорциональна составляющей функции высоты поверхности с пространственной частотой ________________.
Можно еще и иначе осмыслить этот результат. Волновой вектор падающего излучения содержит горизонтальную составляющую _______________________, а вектор отраженного излучения — горизонтальную составляющую _______________ так что член _____________ представляет собой просто разность между горизонтальными составляющими. Можно поэтому сказать, что составляющая амплитуды рассеянного отражения пропорциональна составляющей пространственной частоты профиля поверхности, для которой пространственная частота соответствует изменению горизонтальной составляющей вектора излучения.
До сих пор мы полагали, что третий и последующие члены разложения в степенной ряд (3.48) пренебрежимо малы по сравнению с первыми двумя членами. Если это так, то соответствующее явление носит название рассеяние Брэгга. Очевидно, что при этом должно выполняться условие что эквивалентно условию
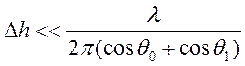
Следовательно, поверхность должна удовлетворять критерию гладкости Рэлея (3.47). Механизм рассеяния Брэгга в значительной степени определяет отражение микроволнового излучения от водной поверхности с небольшими неровностями (порядка 1 см), особенно когда структура этих неровностей содержит доминантную пространственную частоту, и в этом случае рассеяние Брэгга называют резонансным.
Мы пока также полагали, что высотная координата поверхности z зависит только от х. Более общее представление для случая двумерных изотропических поверхностей, более или менее удовлетворяющих изложенным выше аргументам, приводит к следующему выражению для коэффициента обратного рассеяния σ°:
![]() (3.51)
(3.51)
В этом выражении ________— коэффициент обратного рассеяния при pp-поляризации (так, например, р = Н означает НН-поляризацию, т. е. что падающие и отраженные лучи поляризованы в горизонтальной плоскости). Далее, ___________— угол падения излучения, L — интервал корреляции по поверхности (т. е. как бы «ширина» охвата нерегулярностей, несущих всю информацию о спектре пространственных частот) и, наконец, ____________ — мера отражательной способности поверхности при угле падения излучения __________. Если излучение обладает поляризацией вида НН, то
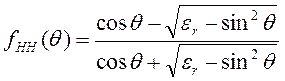 (3.52.1)
(3.52.1)
что фактически является коэффициентом отражения Френеля для излучения, падающего под углом ____________ из вакуума на поверхность, ограничивающую среду с (комплексной) диэлектрической постоянной _________. В случае излучения с VV-поляризацией соответствующая формула имеет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.