Взаимодействие электромагнитного излучения с веществом, страница 14

На рис. 3.18 показано распространение излучения в направлениях + z и — z сквозь три соседних параллельных слоя толщиной _____________ каждый. Будем использовать символы F+ и F- для обозначения плотности потока излучения, распространяющегося в соответствующих направлениях. Когда излучение попадает на один из этих слоев, то часть его __________________ поглощается, а часть ________________________— рассеивается. Допустим, что при рассеянии вся часть излучения отражается в обратную сторону, так что доля излучения, прошедшего сквозь слой, составляет _______________________________________.

Согласно рис. 3.18, плотность потока F+ в среднем слое складывается из части, прошедшей в прямом направлении

сквозь нижний слой, и части, отраженной (рассеянной) в обратном направлении, и мы можем записать:

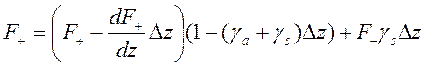
Пренебрегая членами с _______________, после преобразований получим:

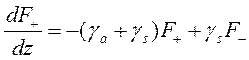                                  (3.61.1)                        

Это уравнение интуитивно понятно. Оно показывает, что излучение теряет часть энергии вследствие поглощения и рассеяния при прямом ходе и восполняет часть за счет рассеяния при обратном ходе. Для варианта, когда излучение распространяется в противоположном направлении, соответствующее уравнение имеет вид:

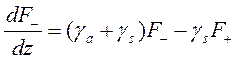                                   (3.61.2)

Обратите внимание на сумму коэффициентов поглощения и рассеяния, стоящую в этих уравнениях и имеющую очень важное значение для описания распространения излучения, так как она характеризует потерю энергии излучения в прямом направлении. Комбинацию поглощения и рассеяния называют аттенуацией, или ослаблением (угасанием), и вводят коэффициент ослабления

                                                                                                                (3.62)

Уравнения (3.61) могут быть использованы для исследования важных свойств пространственного рассеяния. Рассмотрим бесконечно толстый слой материала, обладающего постоянными коэффициентами поглощения и рассеяния, на который нормально падает излучение с единичной плотностью потока. Чтобы максимально упростить задачу, будем считать коэффициент отражения поверхности этого слоя нулевым, так что основную роль играет только объемное рассеяние. Такая ситуация описывается уравнениями (3.61.1) и (3.61.2) в области z  0 и при граничных условиях:

Нетрудно показать, что решения имеют вид:

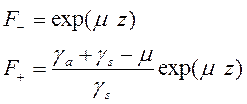
Где

коэффициент интенсивности отражения равен

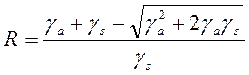                                              (3.63)

График этой функции, зависящей только от соотношения между  и , показан на рис. 3.19.

Как следует из рис. 3.19, если коэффициент рассеяния намного больше коэффициента поглощения, то объемное рассеяние велико. Это объясняет, почему многие из рыхлых материалов, как, например, снег, облака или поваренная соль, имеют белый цвет. Оптическое поглощение в слое чистого льда толщиной 1 м невелико, но если лед состоит из мелких снежных гранул размером всего 1 мм, то световые лучи будут испытывать порядка 2000 пересечений границы лед—воздух. Рассеяние может происходить при каждом таком переходе, и хотя в каждом случае потери невелики, суммарный эффект оказывается значительным. При малом коэффициенте поглощения в видимой части спектра, как это имеет место для льда, воды и соли, материал выглядит как белый.