Взаимодействие электромагнитного излучения с веществом, страница 8

Мы уже видели, что существуют различия между свойствами рассеяния очень гладкой поверхностью и поверхностью Ламберта, являющейся как бы идеально шероховатой. Понятно, что для определения того, какая из этих моделей более подходит для описания свойств реальной поверхности, нужно ввести некий критерий, который бы характеризовал степень шероховатости. Обычно для этой цели используют критерий Рэлея, который мы проанализируем в этом параграфе.

На рис. 3.10 схематически изображен случай падения излучения под углом _______ на нерегулярную поверхность и его зеркального отражения под тем же углом. Рассмотрим два луча: один из них отражается от базовой плоскости, а другой — от плоскости, расположенной на высоте ________ относительно базовой. После отражения разность расстояний, пройденных этими лучами, будет равна_________________, так что разность фаз между ними составит

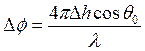
где ______ — длина волны излучения.

Если мы теперь в качестве ________ примем среднее квадратическое отклонение (СКО) высотного положения точек поверхности относительно базовой плоскости, то _________ примет величину СКО колебаний фазы отраженных лучей. Поверхность можно считать достаточно гладкой и дающей спекулярное (почти зеркальное) рассеянное отражение, если _________ не превышает принятого предельного значения порядка 1 радиана. Критерий Рэлея предусматривает это предельное значение равным /2. Следовательно, поверхность может считаться достаточно гладкой, если

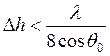                                                 (3.47)

Из уравнения (3.47) следует, что поверхность может считаться достаточно гладкой при нормальном падении лучей, если ее неровности по высоте меньше, чем λ /8 (или, скажем, λ /25). Другой аспект, на который нужно обратить внимание при анализе уравнения (3.47), — это зависимость от ______. Критерий гладкости легче удовлетворить при больших значениях ______, чем в случае нормального падения лучей, так что сравнительно неровные поверхности могут на практике рассматриваться как достаточно гладкие при скользящем облучении.

3.3.4. Модели микроволнового обратного рассеяния

Это очень большая и важная область, в которой еще продолжаются исследования. Математические разработки моделей очень сложны, так что мы можем представить лишь обзор их основных принципов.

3.3.4.1. Модель малых возмущений

Самый удобный путь для начала знакомства с проблемой рассеяния микроволн от шероховатой поверхности — это изучение модели малых возмущений. В сущности, она представляет собой обобщение теории дифракции Фраунгофера на рассеяние шероховатой поверхностью, когда взаимодействие падающего излучения с поверхностью используется для расчета поля исходящего излучения вблизи поверхности. Далее, можно представить, что это поле наведено от падающего однородного излучения фиктивным экраном, изменяющим как амплитуду, так и фазу, и рассчитать поле как дифракцию Фраунгофера от этого экрана.

Чтобы показать, как это все проделать, не вникая при этом глубоко в математические детали, рассмотрим поверхность z(x, у), у которой высотная координата z зависит только от х и которая отражает наверх все падающее излучение (т. е. ее диффузное альбедо равно 1). На рис. 3.11 показаны лучи, падающие на поверхность под углом _________,  и отраженные от нее под углом____________. Лучи АО и О В длиной соответственно а и b примем в качестве базовых, относительно которых будем рассчитывать изменения фаз других лучей. Точка Р принадлежит поверхности, она имеет координаты х, z(x). Используя простые тригонометрические формулы, найдем, что длина луча CP составляет

а длина луча PD —

точке D относительно базового луча будет равна:

где

а k — волновое число излучения.