Энергетическая освещенность (Е) поверхности равна _________. Обозначив через __________________ энергетическую яркость излучения, рассеянного в направлении ____________, введем понятие двумерной функции распределения коэффициента отражения (ДФРКО) R, определяемой выражением:
(3.35)
Эта величина измеряется в единицах (ср-1). Иногда ее также обозначают символами _______ или _______. При рассмотрении радарных систем вместо ДФРКО вводится эквивалентная величина бистатичный коэффициент рассеяния_____________, являющаяся безразмерной и связанная с R соотношением:
(3.36)
На практике большинство радарных систем регистрируют только обратное рассеяние — составляющую, противоположно направленную падающему излучению. В этом случае ______________ и ________________, а в качестве характеристики доли возвращаемой доли рассеянного излучения используется безразмерный коэффициент обратного рассеяния _________, определяемый соотношением:
(3.37)
ДФРКО является функцией направлений падающего и отраженного излучений (в отличие от _________, зависящего только от угла падения излучения, поскольку угол отражения — тот же). Поэтому было бы более правильным записывать ее как функцию четырех аргументов __________________________.Такая форма полезнее в том смысле, что помогает уяснить взаимно-обратную связь ДФРКО:
(3.38)
но из соображений компактности мы будем писать просто R, имея при этом в виду наличие аргументов. В большинстве случаев поверхность обладает благоприятными свойствами с точки зрения учета зависимостей от азимута излучения: вместо учета азимутальных углов ф0 и ф1 бывает достаточно определить зависимость от ____________________, а часто учетом азимута можно вообще пренебречь.
Отражательная способность поверхности _______ является функцией только направления падающего излучения. Она определяется отношением энергии рассеянного отражения к общей энергии падающего излучения:
где М — энергетическая светимость поверхности. Подставляя выражение (2.24) для М, получим:
(3.39)
Отражательную способность поверхности еще иначе именуют альбедо (от латинского «белизна»); она связана с излучательной способностью ___________ в направлении _________________ соотношением:
(3.40)
Используют еще понятие диффузного альбедо_______, называемого также полусферным альбедо, определяя его как среднее значение _______ для излучения, приходящего со всевозможных направлений полусферы. В таком случае он дает отношение общей энергии рассеянного отражения к общей энергии падающего излучения в предположении изотропности его распределения. Значит, поскольку энергетическая яркость постоянна, мы можем обозначить ее как ________, так что вклад ______ в энергетическую освещенность в направлении ________ составит:
Вклад dM в энергетическую светимость в направлении _________ составит, следовательно,
Итак, энергетическая светимость будет равна
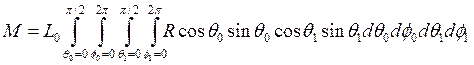
а энергетическая освещенность
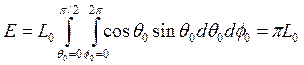
Для диффузного альбедо, определяемого в данном случае отношением М/Е, получим (слегка упрощая формулу с использованием уравнения (3.39)):
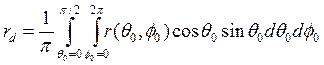(3.41)
3.3.2. Простые модели поверхностного рассеяния
Если рассеивающая поверхность очень гладкая, то ее свойства подобны зеркалу. В этом случае мы имеем дело с так называемым спекулярным рассеиванием, или спекулярным отражением (от латинского specelem — зеркало). Излучение, приходящее с направления ____________, отражается только в направлении ___________ и _________________, как это схематично показано на рис. 3.9, а. Следовательно, ДФРКО здесь является дельта-функцией, которая имеет вид:
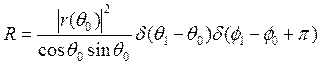(3.42)
где ________ — амплитудный коэффициент отражения Френеля, соответствующий углу падения______. Подставляя это выражение в (3.39), найдем отражательную способность _____ при угле падения_________:
как этого и следовало ожидать, а с учетом уравнения (3.41) получим диффузное альбедо:
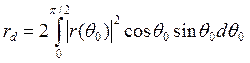
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.