Для дождевых капель х = 0,63. Это, конечно,
слишком большая величина для расчета с достаточной точностью по формуле (3.81)
сечения ослабления, которое составляет 4,78 • 10-6 м2. Но формула (3.82) дает довольно хорошую оценку сечения рассеяния 1,40![]() 10-6 м2 (действительное значение составляет 1,76 • 10-6 м2).
Сечение поглощения здесь составляет 3,02 • 10-6 м2, а соответствующие коэффициенты принимают следующие значения: рассеяния — 1,76
10-6 м2 (действительное значение составляет 1,76 • 10-6 м2).
Сечение поглощения здесь составляет 3,02 • 10-6 м2, а соответствующие коэффициенты принимают следующие значения: рассеяния — 1,76![]() 10-4 м-1 (0,8 дБ/км); поглощения — 3,02
10-4 м-1 (0,8 дБ/км); поглощения — 3,02![]() 10-4 м-1 (1,3 дБ/км); ослабления — 4,78 • 10-4 м-1 (2,1
дБ/км). Хотя рассеяние здесь все-таки ниже поглощения, оно составляет
значительную величину, что иллюстрирует возможность мониторинга дождя при
помощи наземных дождевых радаров.
10-4 м-1 (1,3 дБ/км); ослабления — 4,78 • 10-4 м-1 (2,1
дБ/км). Хотя рассеяние здесь все-таки ниже поглощения, оно составляет
значительную величину, что иллюстрирует возможность мониторинга дождя при
помощи наземных дождевых радаров.
3.4.3. Простые модели объемного рассеяния
Из содержания предыдущих разделов должно быть вполне понятно, что объемное рассеяние представляет собой сложную в математическом плане проблему и что нереально создать единую модель, которая охватила бы все возможные случаи. Поэтому в данном параграфе мы рассмотрим только одну практическую модель объемного рассеяния. Изначально она была разработана для микроволнового обратного рассеяния от снежного покрова, и ее основные положения содержатся в работе Stiles и Ulaby (1980).
Схематически ситуация показана на рис. 3.22. Излучение падает на снежный покров под углом θ к нормали, и часть Т(θ) падающей энергии пересекает его верхнюю границу. Здесь
|
|
где _______________ — коэффициент Френеля.
Это излучение преломляется под углом θ' относительно нормали в соответствии с законом Снеллиуса.
Проходя сквозь слой снега, излучение подвергается объемному рассеянию. Из уравнения (3.63) следует, что величина энергии, отраженной от бесконечного слоя рассеивающей среды, согласно простой одномерной модели зависит только от отношения
.
Очевидно, для обратного рассеяния бесконечной трехмерной средой можно записать аналогичное соотношение:
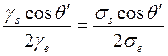
где коэффициент (cos![]() ')/2 введен для учета той части энергии, которая направлена в
сторону обратного рассеяния.
')/2 введен для учета той части энергии, которая направлена в
сторону обратного рассеяния.
Но на самом деле среда не бесконечна, а обладает глубиной d. Оптическая длина пути от снежной поверхности до нижней границы слоя равна
![]()
а оставшаяся доля энергии после двукратного прохождения этого пути (туда и обратно) составляет _________________________. Если эта доля равна нулю, то слой
|
|
|
Рис. 3.22. Объемное рассеяние микроволнового излучения снежным слоем (схема). |
среды можно считать бесконечным, а объемное рассеяние полным; если же эта доля равна 1, то среда прозрачна и объемное рассеяние вообще отсутствует. Итак, мы можем записать выражение
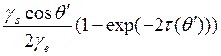
для подсчета той доли падающей в снежный слой энергии, которая отражается обратно вследствие объемного рассеяния. Эта часть излучения снова пересечет границу снег—воздух, и, следовательно, наше выражение для объемной составляющей коэффициента обратного рассеяния примет вид:
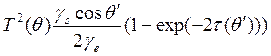
Чтобы наша модель была полной, нужно еще учесть составляющую поверхностного рассеяния и составляющую, образующуюся при рассеянии на границе снег—грунт. Последнюю можно выразить формулой
![]()
учитывая, что излучение дважды пересекает границу снег—воздух и дважды проходит оптический путь _______________. Таким образом, окончательная формула принимает вид:
|
|
(3.85) |
Следует оговориться, что на самом деле это очень упрощенная модель объемного рассеяния, которая не учитывает среди прочего многократное рассеяние. Тем не менее она иллюстрирует основные подходы, используемые при построении подобных моделей.
3.5. Отражение и излучение реальных материалов
Мы уже рассмотрели более или менее детально факторы, влияющие на отражение электромагнитного излучения от твердых и жидких поверхностей, а теперь попытаемся применить эти идеи для понимания отражательных свойств некоторых реальных материалов. Далее мы сможем также рассмотреть излучательные свойства в наиболее важных частях электромагнитного спектра — тепловом инфракрасном и микроволновом. Описание в этом разделе будет довольно сжатым. Более полное изложение можно найти, например, в работе Elachi (1987).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.