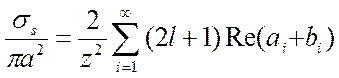Взаимодействие электромагнитного излучения с веществом, страница 18

                            (3.80)                                                         

где ___________, и называются коэффициентами Ми; они зависят от комплексного коэффициента преломления и от величины х. Выражения (3.79) и (3.80) можно разложить в степенные ряды по х. Первые члены этих рядов имеют вид:

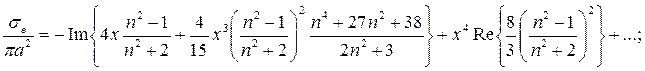       (3.81)

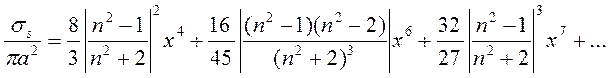          (3.82)

Мы можем трактовать первый член уравнения (3.81) также как результат, полученный для сечения поглощения в модели очень малой сферы, а первый член уравнения (3.82) — для сечения рассеяния Рэлея.

На рис. 3.21 показана зависимость отношений (________________) и (__________________) от х при значении коэффициента преломления n = 5,67 — 2,88i. При малых значениях х (область рассеяния Рэлея) сечение рассеяния пропорционально величине ______________, а сечение поглощения пропорционально х. На рисунке также видно, что при значениях х, близких к 1, оба сечения достигают максимума, примерно равного геометрическому сечению, а затем практически не меняются, испытывая лишь небольшие колебания. Кривыми серого цвета на рис. 3.21 показаны асимптотические продолжения за пределами малых значений х. Для сечения рассеяния нанесена только кривая, рассчитанная по формуле Рэлея, так как она дает адекватную аппроксимцию для значений х вплоть до 1. Для сечения ослабления (аттенуации) показан график, рассчитанный как по полной формуле (3.81) (кривая линия), так и с использованием только ее первого члена (прямая).

Наконец, нам необходимо исследовать, как сечения поглощения и рассеяния, определенные для отдельных частичек, связаны с коэффициентами поглощения и рассеяния. Рассмотрим тонкий слой материала, имеющий площадь сечения А и толщину Δz, на который падает по нормали излучение с плотностью потока F. Материал содержит N частичек на единицу объема, у каждой из которых сечение поглощения равно ___________ и сечение рассеяния — ____________. Понятно, что всего частичек в слое _____________, так что полное количество поглощенной энергии составляет ___________________ (при условии, что толщина слоя Δz достаточно мала). Стало быть, плотность потока уменьшается на ___________________________, а коэффициент поглощения согласно уравнению (3.60) равен

                                                                   (3.83)

Аналогично рассуждая, найдем коэффициент рассеяния:

                                                     (3.84)

В качестве примера рассмотрим поглощение и рассеяние водяными капельками 1 -сантиметрового микроволнового излучения. Возьмем два гипотетических, но близких к реальности варианта:

облачный массив, в котором типичный радиус капелек равен а = 2•10-5 м, а их концентрация N = 2 • 107 м-3;

несильный дождь, при котором а = 1 мм и N = 100 м-3.

При длине волны 1 см показатель преломления воды ____ равен  5,67 — 2,88i, так что при характерном для облачных капель  х = 0,0126 формула (3.81) дает __________= 3,58 • 10-12 м2, а формула (3.82) ______________= 7,73 • 10-17 м2. (Фактически для получения этих значений с достаточной точностью можно ограничиться только первыми членами указанных формул.) Для сечения поглощения получим:

____________________________=3,58  10-12  м2. Умножив это значение сечения на концентрацию капель, получим коэффициент рассеяния для облака 1,55 • 10-9 м-1 и коэффициенты поглощения и ослабления 7,16 • 10 -4 м-1 (примерно 0,3 дБ / км).