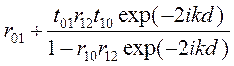Взаимодействие электромагнитного излучения с веществом, страница 13

                                                (3.59)

На рис. 3.17 показан ход этой функции (точнее говоря, энергетического коэффициента отражения, являющегося ее квадратом) в зависимости от толщины слоя d. Для среды 1 принято ____________________, а среда 2 полагается идеально отражающей: ______________. Частота излучения принята равной 1 ГГц. (Указанные значения диэлектрической постоянной не относятся к какому- то конкретному материалу — они взяты просто для примера). На рисунке видно, что когда толщина слоя среды 1 приближается к нулю, энергетический коэффициент отражения становится равным значению на границе между средами 1 и 2. Если слой среды 2 имеет значительную толщину, то энергетический коэффициент отражения близок к значению на верхней границе среды 1. Это легко понять, глядя на рис. 3.16. При большом значении d энергия луча В при прохождении сквозь среду 1 падает почти до нуля, так что ничего не остается для отражения в качестве луча С. Пользуясь формулами

(3.12) и (3.15), можно найти, что абсорбционная длина в среде 1 составляет 0,076 м, и мы видим на рис. 3.17, что указанная выше ситуация практически достигается при толщине слоя, равном примерно пятикратному значению абсорбционной длины. На рис. 3.17 также видно, что кривая коэффициента отражения испытывает периодические колебания, амплитуда которых затухает с увеличением толщины слоя d. Это объясняется интерференцией взаимодействующих лучей.

Хотя мы рассмотрели только простой пример, его анализ ясно показывает, что если под слоем среды 1 нет слоя с другой средой (или, говоря иначе, если слой среды 1 имеет значительную толщину), проникшее в среду 1 излучение не отразится из нее обратно. В этом случае возможно только поверхностное рассеянное отражение. Это, однако, справедливо лишь для однородной среды. Если же среда неоднородна («комковата»), то излучение может рассеиваться на неоднородностях. Это явление будет рассмотрено в следующем параграфе.

3.4.1. Уравнение переноса излучения

Для начала создадим модель поведения излучения при наличии как поглощения, так и рассеяния. С явлением поглощения мы уже знакомы. В п. 3.1.1 было дано определение абсорбционной длины и показано, что (согласно уравнениям (3.14) и (3.15)) при распространении излучения в направлении z в среде, обладающей абсорбционной длиной _____________, плотность потока F определяется соотношением:

где F0 — постоянная. Это выражение можно также записать в виде дифференциального уравнения:

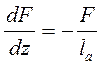
которое имеет смысл, если ___________ зависит от z, но чаще это уравнение записывают в виде:

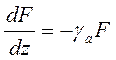                                                 (3.60)

где ___________________ — коэффициент поглощения.

Смысл этого уравнения проще всего пояснить на примере, в котором излучение с плотностью потока F падает нормально на тонкий слой поглощающего материала толщиной Δz. Несколько преобразовав уравнение (3.60), найдем, что т. е. доля энергии поглощенного слоем материала излучения составляет ______________________. Эта доля, как и ожидалось, пропорциональна толщине слоя (если слой тонкий), а ______________представляет собой коэффициент пропорциональности.

Понятие рассеяния может быть определено как отклонение хода электромагнитного излучения без поглощения, происходящее вследствие его взаимодействия с частицами (электронами, атомами, молекулами или более крупными частицами) или с жидкой либо твердой поверхностью. Природу рассеяния частицами мы рассмотрим в следующем параграфе, а пока что определим коэффициент рассеяния. Его смысл тот же, что и коэффициента поглощения: тонкий слой материала толщины Δz рассеивает часть _________________ энергии падающего на него излучения, где __________ и есть коэффициент рассеяния. Конечно, рассеянное излучение не «пропадает», в отличие от поглощенного, и наша задача — проследить его путь. Чтобы понять, как работают уравнения переноса излучения, рассмотрим сначала их упрощенную одномерную версию.