Взаимодействие электромагнитного излучения с веществом, страница 16

В заключение рассмотрим решение уравнения (3.71) в случае, когда _________ не будет константой, потому что непостоянна температура. Это может быть, например, модель зондирования температуры воздуха, где яркостная температура идущего вверх излучения измеряется в точке выше основного объема земной атмосферы и используется, чтобы делать выводы о распределении температуры внутри атмосферы. В этом случае гораздо проще работать с оптической толщиной, а не с позицией z. Из уравнения (3.70) можно отметить наличие монотонной взаимосвязи между _______________и  z. Основываясь на этом, решение уравнения (3.71) можно написать как

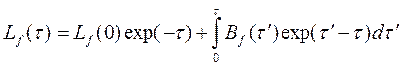                           (3.73)

или, в случае если аппроксимация Рэлея—Джинса имеет силу, как

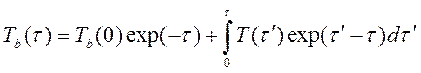                       (3.74)

Как и раньше, возможно интуитивное понимание этих уравнений. Для упрощения рассмотрим уравнение (3.74) и примем, что оно применимо к излучению, проходящему вверх от земной поверхности (где z и ______ равны нулю) сквозь атмосферу на некоторое расстояние ____________ (рис. 3.20). Яркостная температура идущего от земной поверхности излучения ___________, общая оптическая толщина пути _________, и тогда первое слагаемое уравнения (3.74) соответствует уравнению (3.69), т. е. представляет поглощение поверхностного излучения. Подынтегральная функция рассматривает некоторую позицию z из условия, что оптическая толщина между этой точкой _____________есть __________. Оптическая толщина между этой точкой и ____________________есть __________________, и мы ожидаем уменьшения вклада от этой точки на фактор ______________________________. Оптическая толщина _________________________ от точки в атмосфере, где возникает излучение, до точки его измерения называется оптической глубиной первой из двух точек.

3.4.2. Поглощение и рассеяние макроскопическими частицами

В п. 3.4.1 была введена концепция коэффициентов поглощения и рассеяния. Они были определены как объемные факторы среды, сквозь которую распространяется излучение, но их происхождение связано с взаимодействием между излучением и частицами, образующими среду. В этом параграфе мы и рассмотрим зависимость коэффициентов поглощения и рассеяния от физических свойств частиц.

Начнем с того, что будем далее полагать размеры частичек гораздо меньшими, чем длины волн излучения, так что электрическое поле в некоторый момент времени можно считать постоянным для всей частицы. Но мы отложим рассмотрение вопросов рассеяния и поглощения отдельными молекулами до гл. 4, в которой излагается распространение излучения сквозь атмосферу.

Полезной концепцией для понимания вопросов поглощения и рассеяния частичками является поляризуимость, которой мы уже касались в п. 3.1.1 и величину которой будем по-прежнему обозначать буквой __________. Она определяется таким образом, что дипольный момент ________, индуцированный в частице при нахождении ее в электрическом поле Е, равен ___________. Направление дипольного момента такое же, как и вектора электрического поля, но в случае колебаний электрического поля, как это происходит при электромагнитном излучении, колебания дипольного момента и электрического поля могут оказаться не в фазе. С учетом этого поляризуемость _____________ в общем случае является величиной комплексной.

Для начала рассмотрим поглощение частичками электромагнитной энергии. Если индуцированный дипольный момент р изменяется со временем, то мгновенная скорость рассеяния энергии составляет Edp/dt. Пусть электрическое поле в окрестностях частички равно

тогда для дипольного момента можно записать:

Напомним, однако, что физический смысл этого комплексного экспоненциального выражения содержится в его вещественной части. Мы можем полагать без потери общности величину _______ вещественной и переписать выражение для Е в виде: