При помощи уравнений (3.61) можно достаточно точно решать задачи только при условии, что рассеянное отражение полностью направлено в сторону, обратную направлению падающего излучения. В общем же случае рассеянное излучение распространяется по всем возможным направлениям, и тогда уже нельзя применять одномерную модель. Для описания этой ситуации нам понадобится учитывать энергетическую яркость излучения и характеризовать его распространение при помощи как направлений, так и координат. Но основные принципы остаются неизменными. Для трехмерного случая и при учете только поглощения и рассеяния уравнения переноса излучения имеют вид:
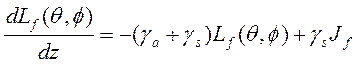 (3.64)
(3.64)
где _________________ — плотность энергетической светимости в направлении __________________, a dz определяет расстояние в этом же направлении. Величина ___________ характеризует излучение в направлении __________________, образовавшееся рассеянием лучей с других направлений______________________
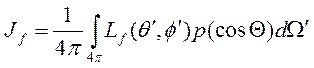 (3.65)
(3.65)
где ______________________________представляет пространственный (телесный) угол, и интегрирование производится по всем направлениям (т. е. по _______ стерадианам); __________________— это фазовая функция рассеяния, она описывает угловое распределение рассеянного излучения на основе угла___________, через который излучение отклонилось
![]() (3.66)
(3.66)
Возможна дальнейшая модификация уравнения (3.64). Мы рассмотрим только одну: для случая излучения абсолютно черного тела. Если излучение находится в тепловом равновесии со средой, через которую оно проходит, к уравнению (3.64) необходимо добавить член, выражающий это излучение:
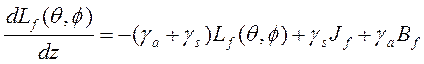 (3.67)
(3.67)
где _____________ является спектральной энергетической яркостью излучения абсолютно черного тела при определенной температуре Т, задаваемой уравнением (2.30):
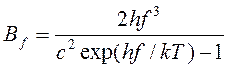 (3.68)
(3.68)
Многие варианты уравнения (3.67) находят важное
применение в различных аспектах дистанционного (удаленного) зондирования. Для
начала рассмотрим случай, в котором имеет значение только поглощение и можно
принять ![]() s и Bf равными нулю. Получается уравнение:
s и Bf равными нулю. Получается уравнение:
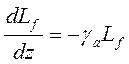
эквивалентное уравнению (3.60). Обратите внимание, что здесь не нужно учитывать направление ___________ из-за отсутствия рассеяния, так что направление не меняется. Если ____________ меняется пропорционально местоположению (координате места) z, то решение этого уравнения можно записать как
![]() (3.69)
(3.69)
где
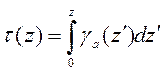 (3.70)
(3.70)
является интегралом коэффициента абсорбции в интервале от 0 до z. Это количество ____________ называется оптической толщиной пути от 0 до z.
Далее снова добавим в модель тепловую эмиссию, продолжая игнорировать рассеяние. Уравнение переноса излучения в этом случае выглядит так:
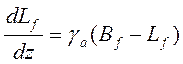 (3.71)
(3.71)
Если частота достаточно низка для применения аппроксимации Рейли— Джинса, это уравнение может приобрести вид:
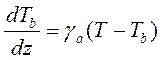
где _______ — яркостная температура излучения, а Т — физическая температура среды, через которую оно проходит. Для константы Т решением этого уравнения будет
![]() (3.72)
(3.72)
Уравнение (3.72), с его очевидной применимостью для коррекции измерений атмосферного поглощения микроволновыми радиометрами, имеет интуитивную корректность. Если излучение проходит через такой незначительный слой поглощающего материала, что показатель ________ имеет малую величину, то яркостная температура вряд ли изменится. Если же оптическая толщина велика, в этом случае яркостная температура выходящего излучения будет равна температуре среды.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.