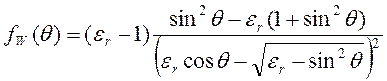Взаимодействие электромагнитного излучения с веществом, страница 10

 

(3.52.2)

Условия, при которых можно применять уравнение (3.51), обычно задают в виде:

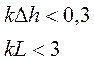                            (3.53.1) и (3.53.2)

хотя они несколько приближенны.

Рис. 3.12. Обратное рассеяние, вычисленное по модели малых возмущений для поверхности с диэлектрической постоянной ε = 10. Все графики рассчитаны с kΔh = 0,3, и они помечены значениями kL. Черные кривые соответствуют поляризации НН, а серые — поляризации VV.

На рис. 3.12 показаны графики обратного рассеяния, рассчитанные с помощью модели малых возмущений для поверхности с _______________. Во всех случаях были приняты одинаковые СКО вариаций высоты Δh. Видно, что эффект возрастания пространственного масштаба неровностей поверхности kL приводит к увеличению спекулярного рассеяния (_____________) за счет уменьшения рассеяния при больших углах. Поскольку СКО наклонов участков поверхности имеет порядок Δh/L, рост величины kL при сохранении неизменным ____________ приводит к уменьшению СКО наклонов, и поэтому не удивительно, что при этом возрастает спекулярная составляющая рассеяния. Эффект изменения _______________, не показанный на рисунке, более очевиден, так как согласно уравнению (3.51) коэффициент обратного рассеяния пропорционален даже________________. Значит, увеличение _______________, скажем, в 10 раз приведет к смещению вниз всех кривых на рисунке на 20 дБ без изменения их наклона.

Автокорреляционные функции

СКО вариаций высоты _______________ является простейшей мерой шероховатости поверхности, но эта величина ничего не говорит нам о распределении масштаба неровностей. Автокорреляционная функция дает эту информацию.

Рассмотрим для простоты одномерную поверхность z (x), где z есть высотная координата в точке х. Среднее значение высоты обозначим как <z>, где угловые скобки означают осреднение по всем значениям х. Выражение для СКО вариаций высоты будет иметь вид:

Автокорреляционная функция вычисляется по следующей формуле:

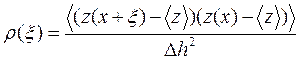
и она является мерой «сходства» значений высот пар точек, расстояние между которыми равно _________________. По определению _________________, а для многих поверхностей__________________. Подходящими моделями для представления автокорреляционных функций являются гауссова

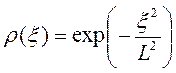
отрицательная экспоненциальная

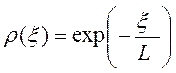
В этих моделях интервал корреляции L является мерой распространения неровностей по поверхности.

Эти идеи можно обобщить и на вариант с двумя измерениями.

3.3.4.2. Модель Кирхгофа

Моделью, примененной Кирхгофом для описания поверхностей со случайно распределенными неровностями, является представление ее в виде совокупности различным образом ориентированных плоскостей, каждая из которых касается поверхности в определенной точке. Такая модель называется аппроксимацией касательными плоскостями. В этом случае поле рассеянного излучения можно рассчитать методами, применяемыми для отражений излучения от плоскости. На практике применяют два варианта модели Кирхгофа: модель со стационарной фазой (или модель геометрической оптики), используемой для шероховатой поверхности, и модель со скалярной аппроксимацией.

В модели со стационарной фазой коэффициент обратного рассеяния определяется по формуле

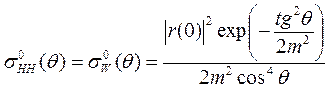                                         (3.54)

где r(0) — коэффициент отражения Френеля для нормально падающего излучения, a m — среднее квадратическое колебание наклонов поверхности. Если свойства поверхности соответствуют гауссовой автокорреляционной функции с интервалом корреляции L и СКО вариаций высоты____________, то

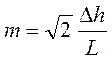                                                 (3.55)

Условиями применимости данной модели являются:

   (3.56.1)

                                                (3.56.2)

 (3.56.3)

Коэффициент обратного рассеяния в модели со скалярной аппроксимацией выражается формулой:

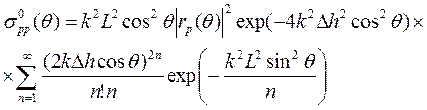                      (3.57)