Спекулярное рассеяние является лишь одним из частных случаев поверхностного рассеяния, и оно происходит от достаточно гладкой поверхности (позже мы рассмотрим, насколько гладкой она должна быть). Другим важным частным случаем является рассеяние на идеально шероховатой поверхности, называемое ламбертовым. Оно обладает тем свойством, что если поверхность облучается равномерно с разных направлений, то отражаемое рассеянное излучение изотропно, и, следовательно, ДФРКО является постоянной величиной. Этот случай схематически представлен на рис. 3.9, б. С помощью уравнений (3.39), (3.41) нетрудно получить для такой поверхности:
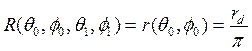(3.43)
Условия рассеяния на реальных поверхностях часто
описываются не с помощью ДФРКО, а путем измерения двумерного коэффициента
отражательной способности (ДКОС). Он представляет собой отношение
энергии потока рассеянного излучения, отраженного в данном
направлении при данных условиях освещенности, к энергии потока, который
образовался бы в условиях ламбертового рассеяния в том же направлении.
Полезность этого критерия состоит в том, что его можно использовать для
характеристики изготавливаемых поверхностей, стремясь приблизить их ДКОС к
единице в широком диапазоне длин волн излучения, а также углов падения и
рассеянного отражения. Наиболее подходящими в этом смысле материалами являются
сульфат бария в виде прессованного порошка, у которого ДКОС составляет более
0,99 при 
< 45° и длинах волн от 0,37 до 1,15 мкм, а также окись
магния, обладающая ДКОС более 0,98 при примерно тех же условиях.
|
|
|
Рис. 3.9. Схематическое изображение различных типов поверхностного рассеяния. Овалы представляют собой полярные диаграммы рассеянного излучения: длина отрезка между точной падения излучения на поверхность и линией овала пропорциональна энергетической яркости рассеянного отражения в соответствующем направлении: а — спекулярное отражение; б — квазиспекулярное рассеяние; в — ламбертово рассеяние; г — модель Миннарта (к = 2); д — модель Хеннея—Гринштейна для прямого рассеяния (в = 0,7); е — модель Хеннея—Гринштейна для обратного рассеяния (0 = — 0,5). |
Хотя ламбертова модель является упрощенной и идеализированной, ее вполне можно использовать, по крайней мере — в первом приближении, для описания реальных поверхностей. Одной из ее модификаций служит модель Миннарта, в которой ДФРКО выражается следующей формулой:
(3.44)
Параметр _____ здесь характеризует степень возрастания или убывания энергетической яркости, рассеиваемой в направлении нормали к поверхности (рис. 3.9, г). Ламбертово рассеяние представляет собой частный случай модели Миннарта при k= 1.
Как уже было отмечено, рассеяние от реальных шероховатых поверхностей может быть описано с помощью моделей Ламберта или Миннарта. Но ни одна из них не учитывает тот факт, что реальные поверхности могут еще дополнительно давать обратное рассеяние (т. е. навстречу падающему излучению) и спекулярное рассеяние. Эти эффекты могут быть учтены путем введения в модели Ламберта или Миннарта эмпирических составляющих, например «квазиспекулярной». Одна из таких модификаций состоит в применении коэффициента Хеннея—Гринштейна в качестве множителя при ДФРКО моделей Ламберта или Миннарта:
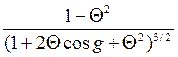(3.45)
где параметр _______ характеризует анизотропию рассеяния, причем ________________ соответствует прямому рассеянию, а — __________________ — обратному. Фазовый угол рассеяния __________ определяется из выражения:
(3.46)
Рисунки 3.9, д, е иллюстрируют рассеяния при ДФРКО, скорректированных типичными значениями коэффициентов Хеннея—Гринштейна.
3.3.3. Критерий Рэлея шероховатости поверхности
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
