








































14. МАГНИТНОЕ ПОЛЕ
14.1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Магнитное поле неразрывно связано с электрическим
током: если где-то протекает ток, то обязательно возникает магнитное поле; если
имеется магнитное поле, то оно обязательно создано током. Основной величиной,
характеризующей магнитное поле, является вектор магнитной индукции ![]() , определяемый по силовому воздействию со
стороны магнитного поля на помещенный в него проводник с током. В расчетах
магнитных полей широко используется вектор напряженности
, определяемый по силовому воздействию со
стороны магнитного поля на помещенный в него проводник с током. В расчетах
магнитных полей широко используется вектор напряженности ![]() . Два указанных вектора связаны между собой
соотношением:
. Два указанных вектора связаны между собой
соотношением: ![]() = mа
= mа![]() , где mа
= m0·mr – абсолютная магнитная проницаемость среды, в которой создано поле; m0 = 4p ·10
-7 Гн/м – абсолют-ная магнитная проницаемость вакуума
(магнитная постоянная); mr –
относи-тельная магнитная проницаемость среды, в которой создано поле. Широкое
распространение получил также магнитный поток, представляющий собой
поток вектора
, где mа
= m0·mr – абсолютная магнитная проницаемость среды, в которой создано поле; m0 = 4p ·10
-7 Гн/м – абсолют-ная магнитная проницаемость вакуума
(магнитная постоянная); mr –
относи-тельная магнитная проницаемость среды, в которой создано поле. Широкое
распространение получил также магнитный поток, представляющий собой
поток вектора ![]() через некоторую поверхность S:
Ф =
через некоторую поверхность S:
Ф = 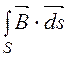 .
.
Основным законом магнитного поля является закон
полного тока. Его интегральная и дифференциальная формы записи: 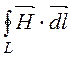 = I, rot
= I, rot![]() =
= ![]() ,
где I–
полный ток, связанный с контуром L;
,
где I–
полный ток, связанный с контуром L;
![]() – плотность тока в
рассматриваемой точке поля.
– плотность тока в
рассматриваемой точке поля.
Используя закон полного тока в интегральной форме, легко получить опорные формулы, по которым можно вычислить напряженность поля, созданного в однородной среде цилиндрическим проводником (задача 14.5) и плоской шиной (задача 14.6).
В областях, не занятых токами (d= 0), магнитное
поле является безвихревым или потенциальным и его можно
рассчитывать с помощью скалярного магнитного потенциала jМ,
причем ![]() = -gradjМ .
Рассчиты-вают jМс помощью уравнения Лапласа Ñ 2j М = 0.
Разность скалярных маг-нитных потенциалов называется магнитным напряжением
= -gradjМ .
Рассчиты-вают jМс помощью уравнения Лапласа Ñ 2j М = 0.
Разность скалярных маг-нитных потенциалов называется магнитным напряжением
UМ12 = j М1 – j М2 = ![]() .
.
Расчёт магнитного напряжения, созданного уединённым проводником в однородной среде подробно рассмотрен в задаче 14.17.
С помощью векторного магнитного потенциала ![]() можно рассчитать магнитное поле в любой
области, в том числе и занятой током. Определяется
можно рассчитать магнитное поле в любой
области, в том числе и занятой током. Определяется ![]() по
уравнению Пуассона Ñ 2
по
уравнению Пуассона Ñ 2![]() = -mа
= -mа![]() , причем div
, причем div![]() = 0 и Ф =
= 0 и Ф = 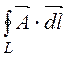 .
.
Граничные условия в магнитном поле: H1t = H2t, B1n = B2n,jМ1=jМ2.
При расчёте магнитных
полей в однородных средах при наличии нескольких источников поля целесообразным
является принцип наложения. При этом найденные от отдельных источников
величины суммируются: скалярные – алгебраически (jМ =S±jМq, UМ
=S±UМq, Ф =S±Фq
и т.д.), векторные – векторно (![]() =S
=S ![]() ,
, ![]() =S
=S![]() ,
, ![]() =S
=S ![]() ).
).
Если магнитное поле создается проводниками, расположенными вблизи границы раздела разных сред, то его расчет упрощается применением метода зеркальных изображений аналогично тому, как это делалось при расчете электрических полей. Коэффициенты неполного отражения (коэффициенты фиктивных токов) при этом вычисляются как
k1 =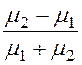 , k2
=
, k2
=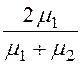 .
.
Индуктивность и взаимная индуктивность контуров:
L=![]() ; M=
; M=![]() =
=![]() .
.
Энергия магнитного
поля контура и её объемная плотность, соответственно, WМ =![]() и wМ =
и wМ =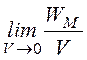 =
=![]() =
=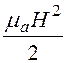 .
.
Во многих случаях индуктивность проще рассчитывать
через энергию магнитного поля L=![]() , а
не через потокосцепление Y (задача 14.9).
, а
не через потокосцепление Y (задача 14.9).
14.2. ИСПОЛЬЗОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ СООТНОШЕ-НИЙ ПРИ РАСЧЁТЕ ПОЛЯ
Задача 14.1. По тонкому проводнику, представляющему собой окружность радиуса а = 1,2 см, протекает ток I= 5 А. Требуется рассчитать магнитную индукцию на оси витка.
Решение
Разместим виток в плоскости x0y декартовой системы координат так, чтобы начало координат совпадало с центром окружности, а направление оси z совпало с положительным направлением нормали к плоскости круга, как это показано на рис. 14.1,а.
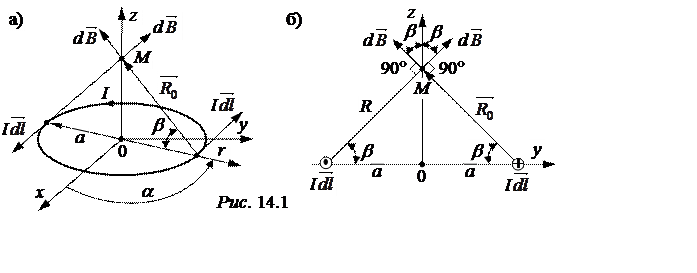 |
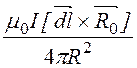 .
.
Между векторами ![]() и
и ![]() угол 90° (рис.
14.1,б), поэтому результат для векторного произведения
угол 90° (рис.
14.1,б), поэтому результат для векторного произведения ![]() = dl·1·sin90° = dl.
= dl·1·sin90° = dl.
Проекция вектора d![]() на
ось z в соответствии с рис. 14.1,б
на
ось z в соответствии с рис. 14.1,б
dBz = dB·cosb, R2 = z2 + a2,
cosb =![]() =
=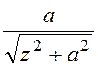 .
.
Элемент длины контура с током dl = a∙da, где a– координата цилиндрической системы координат (рис. 14.1,а).
Подставляя полученные выражения, получаем
dBz =![]()
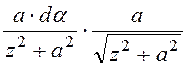 .
.
Магнитная индукция на оси кругового тока
B
=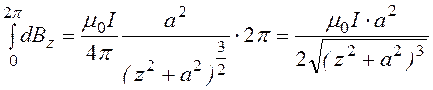 .
.
В плоскости круга (z= 0) численное значение индукции
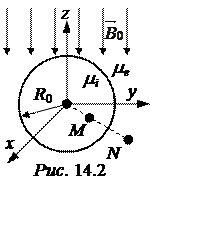 B
=
B
=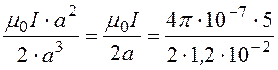 = 26,2·10 -5 тл.
= 26,2·10 -5 тл.
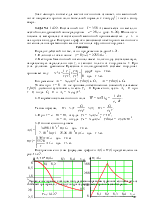
Задача 14.2. В воздухе (me = 1) создано равномер-ное магнитное поле с индукцией В0 = 0,8 Тл. В это поле внесен шар радиусом R0 = 10 см, обладающий магнит-ной проницаемостью mi = 4 (рис. 14.2). Требуется рас-считать магнитную индукцию в точке М(5 см; 120°; 60°) и напряженность магнитного поля в точке N(15 см; 120°; 60°).
Решение
Воспользуемся известным решением уравнения Лапласа в
сферической системе координат [3] 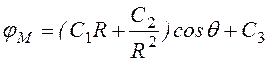 , но сделаем это
дважды: для внутренней области шара и для наружной.
, но сделаем это
дважды: для внутренней области шара и для наружной.
Напряженность магнитного поля будем рассчитывать по
формуле ![]() . В сферической системе координат (см. табл. 11.1)
. В сферической системе координат (см. табл. 11.1)
gradjM =![]() 0
0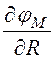 +
+![]() 0
0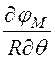 +
+![]() 0
0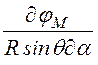 .
.
В рассматриваемом случае
![]() 0
0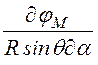 = 0, поэтому
= 0, поэтому ![]() = -
= -![]() 0
0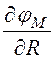 –
–![]() 0
0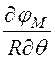 =
=![]() 0HR +
0HR +![]() 0 Hq .
0 Hq .
Заметим, что на границе раздела сред (R=R0) радиальная составляющая HR нормальна к границе, а Hq содержит только тангенциальную составляющую. Магнитная индукция в каждой области В = m rm 0Н.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.