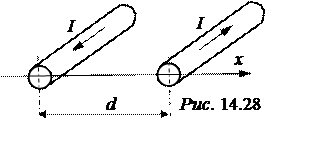
ЗАДАЧА 14.23. Постоянный ток I = 35 А замыкается по двухпроводной линии. Радиус проводов а = 2 мм, расстояние между проводами d = 50 см (рис. 14.28). Провода изготовлены из материала с относительной магнитной проницаемостью m = 4 и находятся в воздухе. Построить графики зависимости векторного магнитного потенциала и напряжённости магнитного поля в функции координаты х.
Решение
При решении задачи применим принцип наложения. Сначала рассчитаем векторный магнитный потенциал и напряженность магнитного поля, созданные каждым проводом в отдельности, а затем алгебраически просуммируем полученные результаты.
При расчете поля от одного, например, левого, провода воспользуемся результатами, полученными в задаче 14.22. Плотность тока в проводах d = I/(pа2) = 2785000 А/м2. Пусть начало координат находится на оси левого провода. Тогда
А1 = - ¼mm 0dх2 = -3,498·х2 Вб/м, Н1 = ½dx = 1,393·106·х А/м;
С3 = - ½m 0dа2 = -7·10-6, С4 = - ¼mm 0dа2 – С3ln(а) = -57,50·10-6.
Таким образом, А¢(х)=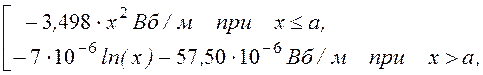
Н¢(х) =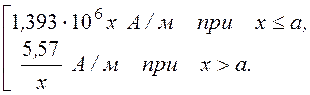
Причём следует помнить, что поскольку провод с током является конструкцией, симметричной относительно плоскости y0z, то функция А¢(х) является чётной, а Н¢(х) – нечётной.3)
Примем, что начало координат находится посередине между проводами. В этом случае формулы А¢(х) и Н¢(х) трансформируются следующим образом (учитывается сдвиг начала координат на d/2):
А¢(х) =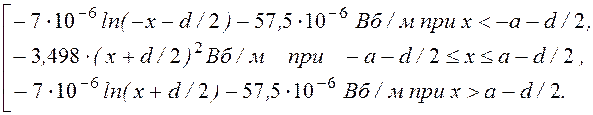
Н¢(х) =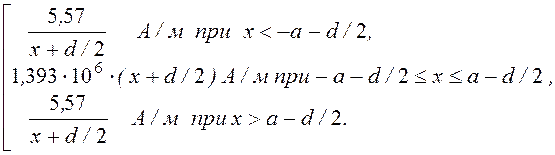
Ток правого провода направлен в противоположную сторону, поэтому знак у функций меняется на противоположный; сдвиг начала координат теперь составляет -d/2. Поэтому
А¢¢(х) =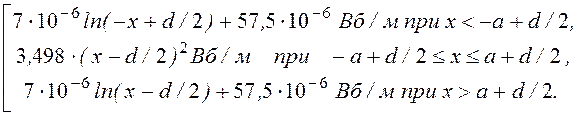
Н¢¢(х) =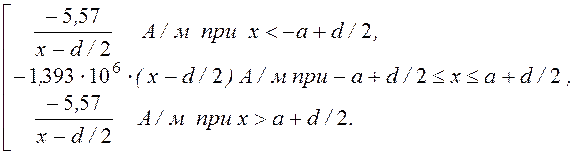
Результирующее поле определяется наложением полей проводов. Как правило, складывать потенциальные функции следует при условии, что они имеют нулевое значение в некоторой одной общей точке. Пусть значение векторного магнитного потенциала равно нулю в начале координат. Тогда А¢(х) следует изменить везде на постоянную величину
N = -А¢(0) = 7·10-6 ln(d/2) + 57,5·10-6 = const, а функцию А¢¢(х) – на величину А¢¢(0) = -N, то есть сумма А(х) = А¢(х) + А¢¢(х) останется неизменной, так как константы N и -N при суммировании взаимно уничтожатся. Окончательно получаем:
А(х) =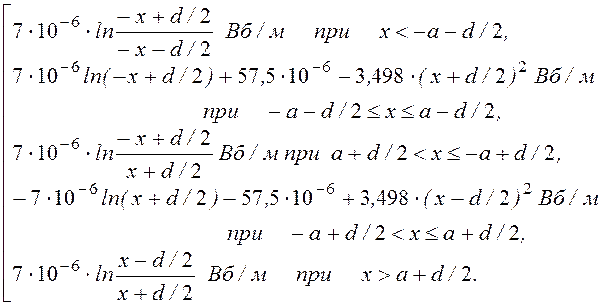
Н(х) = Н¢(х) + Н¢¢(х) =
=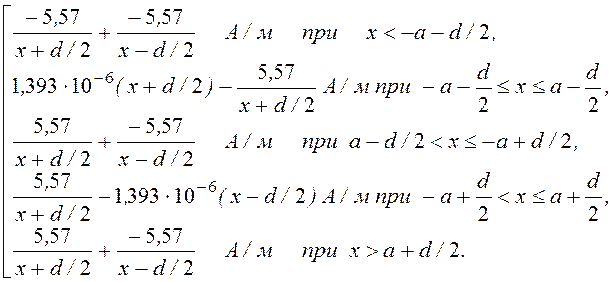
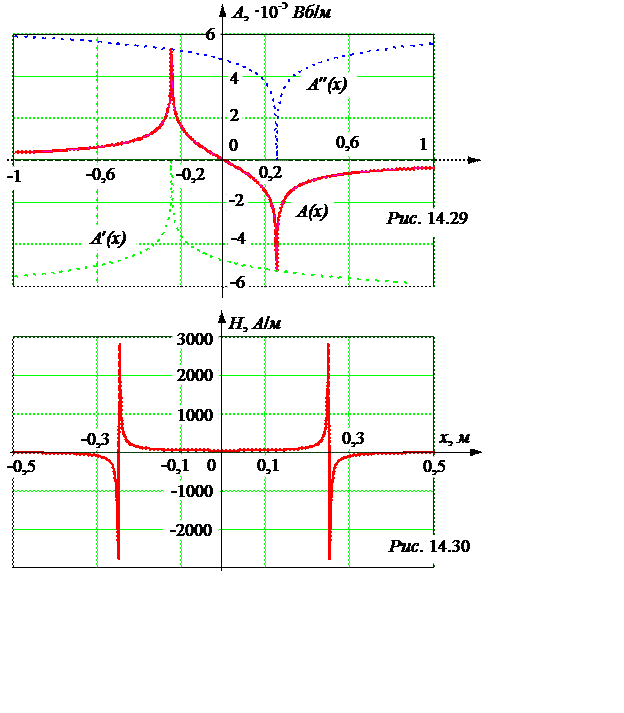
Построенные по этим формулам графики А(х) и Н(х) представлены на рис. 14.29 и 14.30.
 |
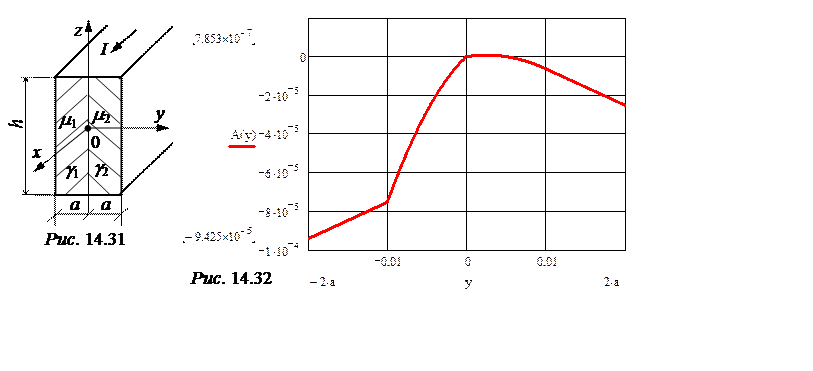
ЗАДАЧА 14.24. По биметаллической шине прямоугольного сечения протекает постоянный ток I = 1500 А (рис. 14.31). Относительные магнитные проницаемости материалов шин m1 = 6m0, m2 = m0, удельные проводимости g1 = 2·107 См/м, g2 = 4·107 См/м. а = 1 см, h= 50 см.
Рассчитать и построить график векторного магнитного потенциала в функции координат.
Ответы: плотности тока d1 = 105 A/м2, d2 = 2·105 A/м2,
A(у) =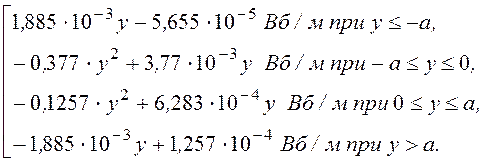
График A(у) представлен на рис. 14.32.
ЗАДАЧА 14.25. По двум параллельным шинам протекают одинаковые
токи I = 200 А
(рис.
14.33). Относительная магнитная проницаемость шин m = 5, окружающая среда – воздух.
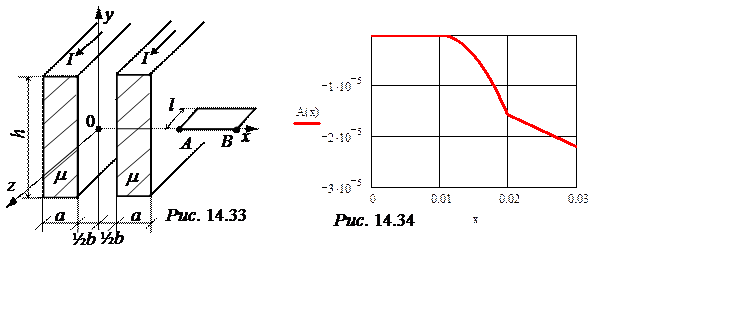
Рассчитать и построить график векторного магнитного потенциала для положительных значений координаты х. Рассчитать магнитный поток через площадь рамки длиной l = 2 м, если А[3 см; 0]; В[5 см; 0 см] и а = 1 см, b = 2 см, h = 40 см.
Ответы: плотность тока в шине d = 5·104 A/м2;
A(х) =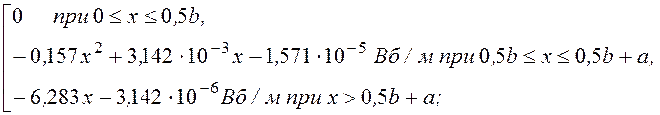
график A(х) представлен на рис. 14.34; A(хВ) = -3,456·10 -5, A(хА) = -2,199·10 -5,
 |
ЗАДАЧА 14.26. Рассчитать и построить графики векторного потенциала и магнитной индукции коаксиального кабеля, изоляция, жила и оболочка которого выполнены из немагнитного материала (рис. 14.35).
r1 = 6 мм, r2 = 14 мм, r3 = 15 мм, I = 200 A.
Ответы: плотности тока d1 = 1,768·106 A/м2, d2 = 2,195·106 A/м2,
A(r) =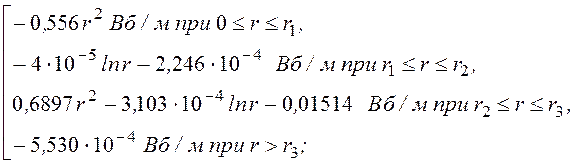
В(r) =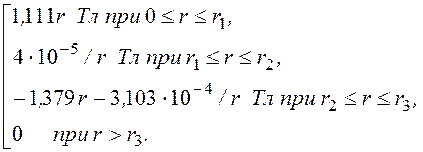
Графики A(r) и В(r) представлены на рис. 14.36.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.