Магнитное поле. Основные теоретические положения, страница 5

Ф₁₂¢= 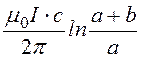;     Ф₁₂¢¢= ;

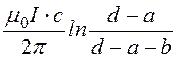Ф₁₂= Ф₁₂¢+ Ф₁₂¢¢= .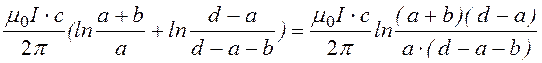

Тогда взаимная индуктивность

M=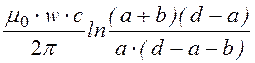 = 2,637·10 ^-5 Гн.

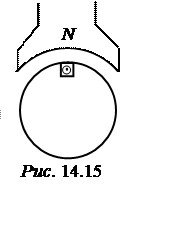ЗАДАЧА 14.14.На рис. 14.15 схематически показан якорь электрической машины, имеющий только один виток. Активная длина якоря   l = 60 см,   наружный диаметр якоря D = 25 см,  диаметр окружности, на которой расположен про-вод,  d = 20 см.  Относительная магнитная проницаемость стали  μ_r = 600.  Ток в витке  I= 100 А.  Считая поле под полюсами однородным с индукцией  B= 1,2 Тл,  определить вращающий момент, действующий на якорь; силу, действующую на провод, и момент этой силы.

Решение

Обозначим индукцию в зазоре слева от провода В_л, а справа – В_п. Так как магнитная проницаемость стали намного больше проницаемости воздуха, то в соответствии с законом полного тока можно считать, что (В_л – В_п)d= m₀I, где d – зазор между статором и якорем.

Пусть при отсутствии тока в якоре индукция в зазоре равна  В,  тогда  В_л + В_п = 2В.Энергия магнитного поля (в единице объема) в зазоре слева от проводника 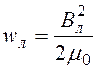 ,  а справа –  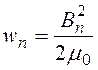.  Приращение энергии при повороте якоря на угол  Δa по часовой стрелке

ΔW=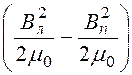2ldΔa=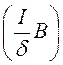ldDΔa= IBlDΔa.

Изменением энергии в стали при повороте якоря на угол  Δaможно пренебречь, так как  μ_r >>1.

Вращающий момент, действующий на якорь,

M = ΔW/Δa = IBlD = 18 Hм.

Силу, действующую на провод в пазу, можно оценить, исходя из следующих соображений. Если паз глубокий, то можно считать, что напряженность магнитного поля в нем приблизительно равна напряженности поля в стали, а индукция в  μ_r  раз меньше, чем в стали. Следовательно, сила, действующая на провод в пазу,    F = BIl/μ_r = 0,12 H,     a момент этой силы  М₀ = Fd = Md/(μ_r D) = 0,024 Hм. 

Таким образом, момент, действующий на провод в пазу, примерно в μ_r  раз меньше момента, действующего на якорь.

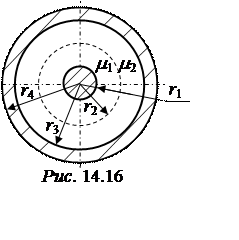
Задача 14.15. По жиле двухслойного коаксиального кабеля (рис. 14.16) замыкается постоянный ток  I = 80 А.

r₁ = 3 мм,   r₂ = 8 мм,   r₃ = 15 мм,   r₄ = 18 мм,   m₁ = 3, m₂ = 8. Жила и оболочка выполнены из немагнитного материала.

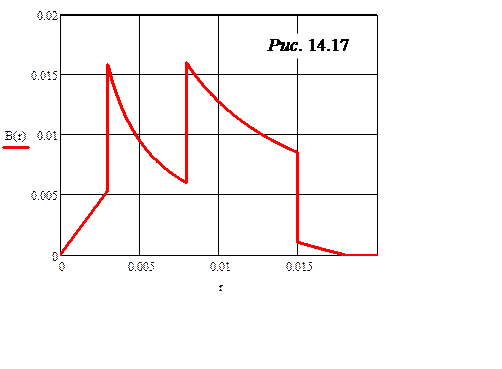
Построить график изменения магнитной индукции по сечению кабеля. Рассчитать внешнюю индуктивность кабеля длиной  l = 25 м,  найти запасённую энергию магнитного поля.

Ответ: В(r) =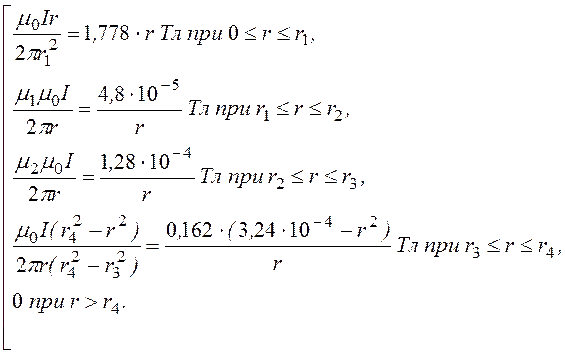  r [м];

график  В(r)  представлен на рис. 14.17;   L_е = 4·10 ^-5 Гн;

W= 0,128 Дж.

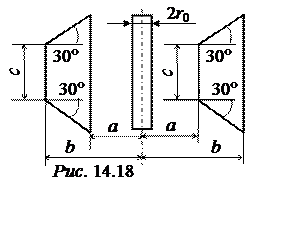
ЗАДАЧА 14.16. Прямолинейный про-водник и две рамки с числами витков  w = 300  находятся в воздухе в одной плоскости (рис. 14.18). Размеры:    r₀ = 3 мм,  а = 5 см,  b = 15 см,  с = 30 см.

1) Рассчитать взаимную индуктивность проводника и правой рамки.

2) Рассчитать взаимную индуктивность проводника и левой рамки.

Ответы:  1)  h(r) = 2·(0,577r + 0,1211) м,

dS = dr·h(r),   B = m₀I/(2pr),     dФ = B·dS = I··(0,577r + 0,1211)·,

Ф =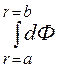= I·7,63·10 ^-8 Bб,   M =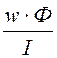= 22,89 мкГн.

2)  h(r) = 2·(-0,577r + 0,2366) м,   dФ = B·dS = I··(-0,577r + 0,2366)·,

Ф =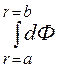= I·8,089·10 ^-8 Bб,   M =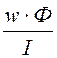= 24,27 мкГн.

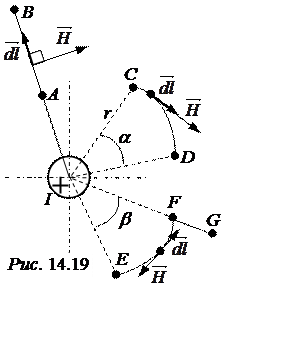
ЗАДАЧА 14.17. Рассчитать магнитные напряжения U_mАВ, U_mСD, U_mЕG поля уединённого проводника с током I в однородной среде с магнитной проницаемостью m_а (рис. 14.19).

Решение

Магнитное напряжение между точками A и B, находящимися на радиальной линии:

U_mАВ =.

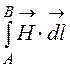Во всех точках отрезка AB угол между векторами  и  равен 90°. Поэтому их скалярное произведение равно нулю, а также равно нулю напряжение    U_mАВ = j_А – j_В = 0.  Скалярные магнитные потенциалы j_А и j_В равны, следовательно, радиальная линия является эквипотенциалью.

Магнитное напряжение между точками С и D, лежащими на дуге окружности:               U_mСD 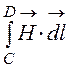 =.  Во всех точках дуги СD угол между векторами  и  равен 0°, скалярное произведение векторов можно заменить произведением их модулей. Величина напряженности   H  одна и та же –   H =,   поэтому  напряженность  можно вынести за знак интеграла, а интеграл от dl даст длину дуги СD:

U_mСD = H·= H·l_CD =·r·a =·a,    a[рад].