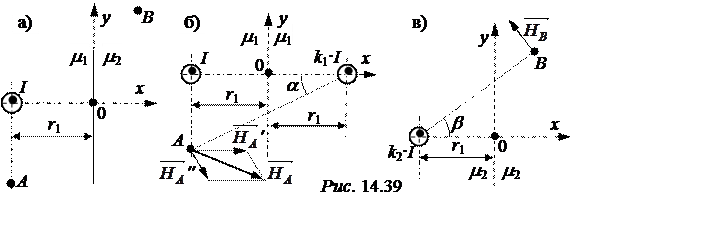
Задача 14.29. Уединённый провод с током I = 10 А находится вблизи границы раздела сред (рис. 14.39,а) с m1 = 2, m2 = 6, r1 = 10 см. Координаты точек хА = уА = -10 см, хВ = 5 см, уВ = 15 см. Требуется:
1. Рассчитать напряжённости магнитного поля в точках А и В, а также магнитное напряжение между ними.
2. Считая, что А и В являются точками сечения длинных сторон прямоугольной рамки длиной l = 1 м и с числом витков w = 100, найти магнитный поток рамки и взаимную индуктивность провода и рамки.
Решение
 |
Коэффициент
неполного отражения k1 =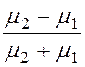 =
=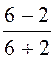 = 0,5.
= 0,5.
Напряженность магнитного поля в точке А:
НА¢ = =
=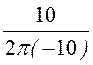 = 0,159 А/см;
= 0,159 А/см;
НАх¢ = НА¢ = 0,159 А/см; НАу¢ = 0;
НА¢¢ =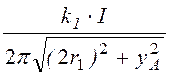 =
=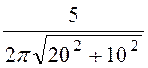 = 0,036 А/см;
= 0,036 А/см;
tga =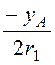 = 10/20 = 0,5, a = 0,4636
рад;
= 10/20 = 0,5, a = 0,4636
рад;
НАх¢¢ = НА¢¢·sina = 0,036·0,4472 = 0,016 А/см;
НАy¢¢ = -НА¢¢·cosa = 0,036·0,8944 = 0,032 А/см;
НА =![]() =
=![]() =
=
= 0,178 А/см.
Магнитное напряжение согласно (14.4):
UmA0 = UmA0¢ + UmA0¢¢ =![]()
![]() –
– 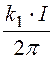 a =
a =![]() –
– ![]() 0,4636
= 2,131 A.
0,4636
= 2,131 A.
Магнитный поток сквозь сечение A0 согласно (14.3):
ФA0 = Ф¢ + Ф¢¢ =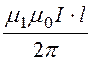 ln
ln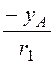 +
+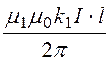 ln
ln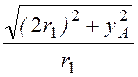 =
=
= 0 +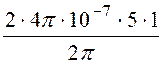 ln
ln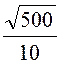 =
1,609·10-6 Вб (направлен сверху вниз).
=
1,609·10-6 Вб (направлен сверху вниз).
2. Расчёт поля в правом полупространстве от границы выполним по рис. 14.39,в.
k2 =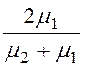 =
=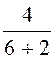 = 0,5;
= 0,5;
НВ =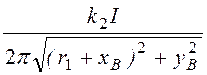 =
=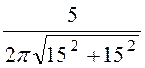 = 0,038 А/см;
= 0,038 А/см;
tgb =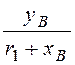 =
15/15 = 1, a = p/4 рад;
=
15/15 = 1, a = p/4 рад;
Um0В
=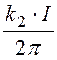 b =
b =![]()
![]() =
0,625 А;
=
0,625 А;
Ф0В =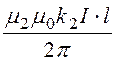 ln
ln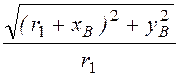 =
=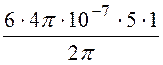 ln
ln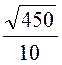 =
=
= 4,512·10-6 Вб (направлен снизу вверх).
3. Окончательно получаем:
- напряжённости поля – НА = 0,178 А/см; НВ = 0,038 А/см;
- магнитное напряжение UmАВ = UmА0 + Um0В = 2,131 + 0,625 = 2,756 А;
- магнитный поток ФАВ = -ФА0 + Ф0В = (-1,609 + 4,512)·10-6 = 2,903·10-6 Вб;
- взаимная индуктивность провода и рамки
М =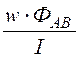 =
=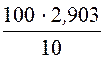 =
29,03 мкГн.
=
29,03 мкГн.
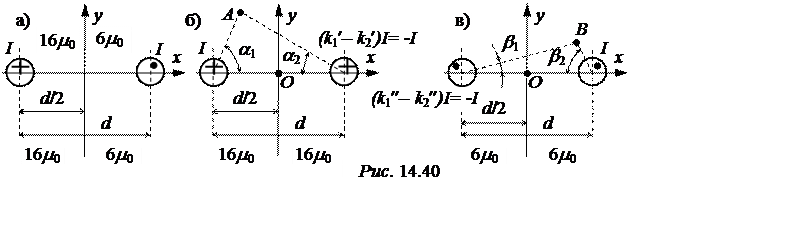
Задача 14.30. По проводам двухпроводной линии, находящимся в разных магнитных средах, протекает постоянный ток I = 130 А (рис. 14.40,a). Радиус проводов r0 = 1 см, d = 50 см. Рассчитать магнитное напряжение между точками А(-15 см; +30 см) и В(20 см; 10 см).
Ответ: коэффициенты неполного отражения:
k1¢ =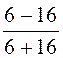 = -0,455, k2¢ =
= -0,455, k2¢ =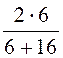 =
0,545, k1¢¢ = -k1¢ = 0,455, k2¢¢ =
=
0,545, k1¢¢ = -k1¢ = 0,455, k2¢¢ =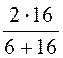 = 1,455;
= 1,455;
углы в радианах, показанные на рис. 14.40,б и в:
a1 = 1,249, a2 = 0,644, b1 = 0,219, b2 = 1,107;
расчётные эскизы для напряжений UmAO и UmOB показаны на рис. 14.40,б и в, соответственно;
 |
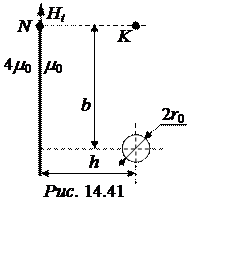
ЗАДАЧА 14.31. Цилиндрический провод ради-усом r0 = 6 мм расположен в воздухе на расстоянии h = 40 см (рис. 14.41) от железобетонной стены с отно-сительной магнитной проницаемостью mr = 4.
Требуется: 1. Определить какого направления и величины необходимо пропустить ток по проводни-ку, чтобы в точке N(b = 30 см) тангенциальная составляющая напряженности магнитного поля составляла Нt = 50 А/м.
2. Рассчитать силу, действующую при этом на 1 пм проводника.
3. По величине и направлению определить магнитную индукцию в точке K.
4. Найти объёмные плотности энергии магнитного поля в точках K и K¢, являющейся зеркальным отображением точки K.
Ответы: I= 490,6 А, ток направлен за плоскость рисунка;
F= 0,0361 Н/м, а проводник притягивается к стене;
ВK = 3,572∙10 -4 Тл; wK = 50,8∙10 -3 Дж/м3, wK¢ = 3,36∙10 -3 Дж/м3.
14.6. Применение ПЭВМ для решения задач
 Применять ПЭВМ целесообразно для решения задач,
требующих большого объёма вычислительной работы. Ниже приведены решения
некоторых подобных задач.
Применять ПЭВМ целесообразно для решения задач,
требующих большого объёма вычислительной работы. Ниже приведены решения
некоторых подобных задач.
ЗАДАЧА 14.32. По проводам трехпроводной воздушной линии протекает постоянный ток I как показано на рис. 14.42. Расстояние между всеми про-водами 2d = 140 см. Радиусы проводов намного меньше d. Требуется рассчитать напряженности магнитного поля в точках А и В, а также магнитное напряжение между ними, если I= 60 А, хА = -10 см; yА = -15 см; хВ = 15 см; yB = 20 см.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.