Магнитное поле. Основные теоретические положения, страница 7

Трубки магнитного потока имеют вид колец вокруг проводника, поэтому магнитный поток сквозь сечение АВ будет равен магнитному потоку сквозь сечение А¢В, где А¢ – точка, удалённая от центра проводника на расстояние r_A, но находящаяся в среде с m₃. Величина магнитного потока согласно (14.3):    Ф =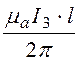ln,     где   I₃ = H₃·r_A·2p,   m_a = m₃·m₀.

Таким образом,

Ф = m₃·m₀·H₃·r_A·l·ln= 6·4p ·10 ^-7··1·ln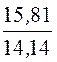= 0,893·10 ^-6 Вб.

Взаимная индуктивность

М =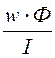==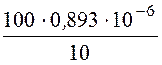 8,93·10 ^-6 Гн = 8,93 мкГн.

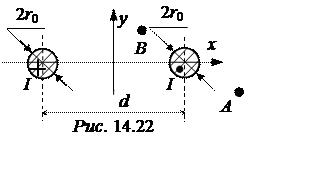
Задача 14.20. Постоянный ток        I = 80 А  замыкается по воздушной двухпро-водной линии (рис. 14.22):

r₀ = 2 мм,  d = 30 см.

Рассчитать поле линии, найти энергию, запасённую между проводами линии длиной    l = 1,5 м.   Найти магнитное напряжение между точками  А[40 см; -10 см]  и  В[10 см; 10 см].

Решение

Расчет поля линии произведем методом наложения. Так, напряжен-ность магнитного поля в любой точке определится как  =¢+¢¢, где ¢ – составляющая напряженности, созданная левым проводом, а ¢¢ –  правым.

В точках, лежащих на оси х, напряженность поля определяется наибо-лее просто, так как составляющие ¢ и ¢¢ сонаправлены (рис. 14.23,а), а каждая из них может быть рассчитана с помощью закона полного тока. Так, в пространстве между проводами

H¢ =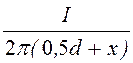;   H¢¢ =;

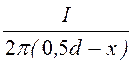H = H¢ + H¢¢ =( +) =·.

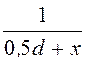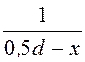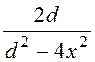Энергия магнитного поля между проводами линии W = ½LI ², где L– внешняя индуктивность линии заданной длины l. Последняя же (см. задачу 14.8):

L=;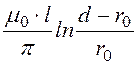

W =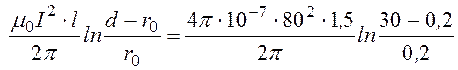= 9,608·10 ^-3 Дж.

Магнитное напряжение между точками А и В также определим с помощью метода наложения  U_mАВ = U_mAB¢ + U_mAB¢¢, где U_mAB¢ –  составляю-щая, создаваемая левым проводом, а  U_mAB¢¢ – правым. В соответствии с (14.4) и рис. 14.23,б

U_mAB¢ =(a₁ + b₁),

a₁ = arctg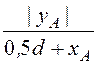= 0,180 рад;      b₁ = arctg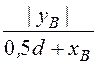= 0,381 рад;

U_mAB¢ =(0,18 + 0,381) = -7,14 A.

Аналогично составляющая  U_mAB¢¢, создаваемая током  правого провода (рис. 14.23,в)

U_mAB¢¢ =(a₂ + ½p+ b₂),

a₂ = arctg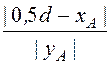= 1,190 рад;     b₂ = arctg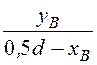= 1,107 рад;

U_mAB¢¢ =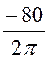(1,190 + 1,571 + 1,107) = -49,25 A.

Тогда        U_mAB = U_mAB¢ + U_mAB¢¢ = -7,14 – 49,25 = -56,39 A.

14.4. РАСЧЁТ ВЕКТОРНОГО МАГНИТНОГО ПОТЕНЦИАЛА И его ИСПОЛЬЗОВАНИЕ

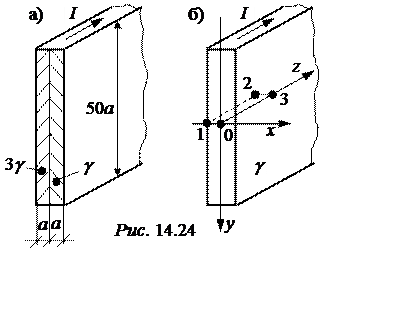
Задача 14.21. Постоянный ток   I = 100 А   замыкается по биметалли-ческой шине (рис. 4.24,a). Шина изготовлена из материала с относительной магнитной проницаемостью m = 6 и находится в воздухе. Удельная проводи-мость слоёв шины 3g и g. Размер  а = 2 мм. Построить графики зависимости векторного потенциала и напряжённости магнитного поля в функции координат. Используя векторный магнитный потенциал, рассчитать магнитный поток, замыкающийся по левой половине шины на единицу длины.

Решение

1. Определим плотности тока в шине (d₁ – в левой половине, d₂ – в правой).

С одной стороны, ток в шине равен  I = d₁·50а² + d₂·50а².

С другой стороны, заметив, что относительно границы раздела сред вектор плотности тока имеет только тангенциальную составляющую, на основании граничного условия     Е_1t = Е_2t  и закона Ома в дифференциальной форме  d =g·E  получаем допол-нительное уравнение  d₁/(3g) = d₂/g  или  d₁ = 3d₂.  Таким образом,  4d₂·50а² = I;

d₂ = I/(200а²) = 100/(200·4·10^-6) = 125000 А/м²;    d₁ = 375000 А/м².

2. Расчёт поля выполним, используя уравнение Пуассона:

Ñ  ² = -m_a·.

Направления осей декартовой системы координат выберем так, как показано на рис. 14.24,б. Из рисунка видно, что вектор плотности тока направлен по оси z, поэтому и векторный магнитный потенциал имеет только одну составляющую – по оси z. Кроме того, так как высота шины значительно больше её толщины, все величины зависят только от одной координаты – x. Таким образом,  А_х = А_у = 0,  == 0. С учетом этого (см. табл. 11.1):    Ñ  ²A =++=.

Произведём двукратное интегрирование этого уравнения для четырех областей поля:

1)   x < -a, 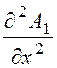        = 0,              А₁ = С₁·х + С₂,

2)  -a £ x £ 0, 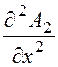   = -m_a·d₁,      А₂ = -d₁·х² + С₃·х + С₄,