Через точку А вокруг шины проведём
прямоугольный контур 1-2-3-4-1 и применим к нему закон полного тока в
интегральной форме: 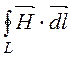 = I.
= I.
В точках, расположенных вблизи поверхностей шины 1-2 и
3-4, создаётся однородное магнитное поле. Поскольку высота шины во много раз
больше её толщины, результатом интегрирования вдоль сторон 1-4 и 2-3 можно
пренебречь. В точках сторон 1-2 и 3-4 направления векторов ![]() и
и ![]() совпадают,
а значение напряжённости Н одинаково. Тогда скалярное произведение
векторов
совпадают,
а значение напряжённости Н одинаково. Тогда скалярное произведение
векторов ![]() и
и ![]() заменяем
произведением их модулей, а Н выносим за знак интеграла как константу.
Получаем:
заменяем
произведением их модулей, а Н выносим за знак интеграла как константу.
Получаем:
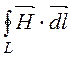 = Н·l12 + Н·l34 = Н·2h = I;
Н =
= Н·l12 + Н·l34 = Н·2h = I;
Н =![]() . (14.2)
. (14.2)
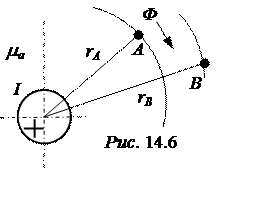
ЗАДАЧА 14.7. Рассчитать магнитный поток, созданный уединенным проводником в однородной среде сквозь прямоугольную рамку AB длиной l, длинные стороны которой параллельны проводнику (рис. 14.6).
Решение
Магнитный поток Ф через рамку АВ
определяется потоком по трубке, ограниченной окружностями с радиусами rА и rВ: Ф =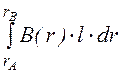 .
.
Но в соответствии с (14.1) Н=![]() ; В(r)=mа·Н =mа·
; В(r)=mа·Н =mа·![]() . Таким образом,
. Таким образом,
Ф =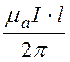 ln
ln![]() .
(14.3)
.
(14.3)
Примечание. Если рамку поворачивать вокруг своей оси, то макси-мальный поток будет проходить сквозь рамку, когда она расположена своей плоскостью перпендикулярно к силовым линиям (по радиальным линиям).
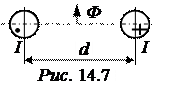
ЗАДАЧА 14.8. Рассчитать внешнюю индуктив-ность двухпроводной линии (рис. 14.7). Радиус проводов и расстояние между ними r0 = 1 см, d= 1 м.
Решение
Внешняя индуктивность линии обусловлена магнитным
потоком между проводами. Так как по проводам протекает одинаковый ток, то и
созданные ими магнитные потоки между проводами равны. Поток от одного провода в
соответствии с (14.3) – Ф =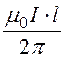 ln
ln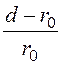 .
.
Искомая внешняя индуктивность на 1 м длины линии:
L
=![]() =
=![]() ln
ln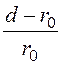 =
=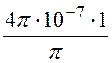 ln
ln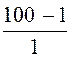 = 1,84·10 -6 Гн = 1,84 мкГн.
= 1,84·10 -6 Гн = 1,84 мкГн.
ЗАДАЧА 14.9. Рассчитать поле и индуктивность коаксиального кабеля (рис. 14.8). По кабелю замыкается ток I.
Решение
Снаружи кабеля поле отсутствует, так как SI = 0. Таким
образом, можно выделить три различные области (обозначены на рис. 14.8,а римскими
цифра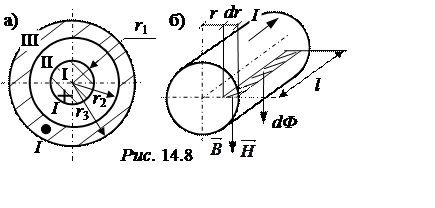 ми) с магнитными проница-емостями mа1, mа2, mа3.
ми) с магнитными проница-емостями mа1, mа2, mа3.
Для расчета поля используем закон полного тока:
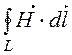 = SI.
= SI.
1. Область I – 0 < r < r1 (рис. 14.8,б). 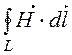 = H·2pr;
= H·2pr;
SI
= I ![]() ; H =
; H =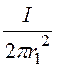 ·r; B = mа1·H
=
·r; B = mа1·H
=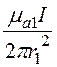 ·r; dФ
= B·dS =
·r; dФ
= B·dS =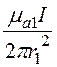 ·r·l·dr.
·r·l·dr.
Так как во внутреннем проводнике магнитный поток dФ сцеплен только с частью тока I,
которая пропорциональна отношению r2/r12, то магнитное потокосцепление dY = dФ·![]() .
.
Внутренняя индуктивность первой области вычисляется по формуле
l1 =![]() =
=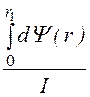 =
=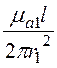 ·
·![]()
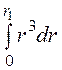 =
=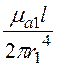 ·
·![]()
![]() =
=![]()
и, как видим, не зависит от радиуса жилы.
2. Область II – r1 < r < r2.
SI
= I; H =![]() ; B =
; B =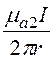 ; dY = dФ = B·dS =
; dY = dФ = B·dS =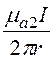 ·l·dr.
·l·dr.
внешняя индуктивность l2 =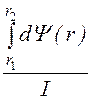 =
= ln
ln![]() .
.
3. Область III – r2 < r < r3.
SI=I
– I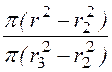 ; H=
; H=![]()
 ; B=
; B=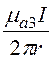
 ; dФ=
; dФ=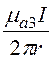
 ·l·dr.
·l·dr.
Этот
поток сцеплен с током I и частью обратного тока, равной I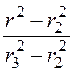 .
.
Поэтому элементарное потокосцепление
dY = dФ·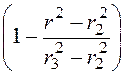 = dФ·
= dФ· .
.
Внутренняя индуктивность третьей области:
l3 =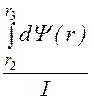 =
=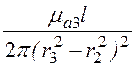
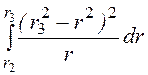 =
=
 =
=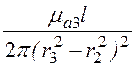 ·[
·[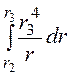 – 2r
– 2r![]()
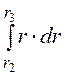 +
+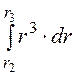 ] =
] =
=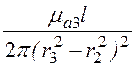 ·[r
·[r![]() ln
ln![]() – r
– r![]() (r
(r![]() –r
–r![]() )+
)+![]() (r
(r![]() –r
–r![]() )] =
)] =
=![]() [
[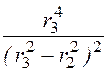 ln
ln![]() –
–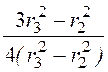 ].
].
Внешняя индуктивность кабеля – lе = l2; внутренняя индуктивность – li = l1 + l3; вся индуктивность – l = l1 + l2 + l3.
Примерный график зависимости Н(r) представлен на рис. 14.9.
1. Область I – 0 < r
< r1. H
=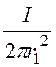 ·r.
·r.
Энергия элементарного слоя dr (рис. 14.8) на расстоянии r от оси:
dW =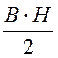 dV = ma1
dV = ma1![]() ·2prl·dr = ma1
·2prl·dr = ma1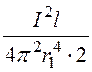 r2·2prdr
= ma1
r2·2prdr
= ma1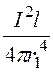 r3·dr.
r3·dr.
L1 =![]() =
=![]()
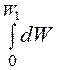 =
=![]() ma1
ma1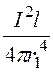
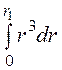 =
=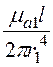
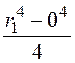 =
=![]() .
.
2. Область II – r1 < r < r2.
SI
= I; H =![]() ; dW = ma2
; dW = ma2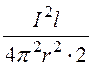 2pr·dr = ma2
2pr·dr = ma2![]()
![]() .
.
L2 =![]() ma2
ma2![]()
![]() =
=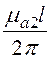 ln
ln![]() .
.
3. Область III – r2 < r
< r3. H =![]()
 ;
;
dW
= ma3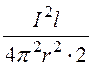
 2pr·dr
= ma3
2pr·dr
= ma3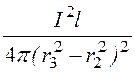
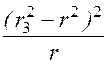 dr.
dr.
L3 =![]() ma3
ma3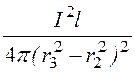 [
[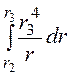 –2r
–2r![]()
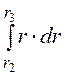 +
+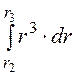 ] =
] =
=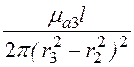 ·[r
·[r![]() ln
ln![]() – r
– r![]() (r
(r![]() –r
–r![]() )+
)+![]() (r
(r![]() –r
–r![]() )].
)].
ЗАДАЧА 14.10. Рассчитать внутреннюю индуктивность прямоуголь-ной шины (рис. 14.10).
Решение
Плотность
тока в шине – d = I/(а·h). В соответствии с законом полного тока Н·2h = d ·2хh,
откуда Н = dх, то есть напряженность Н внутри шины зави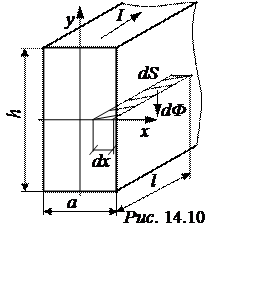 сит от х по линейному закону. На поверхности
шины
сит от х по линейному закону. На поверхности
шины
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.