Магнитное поле. Основные теоретические положения, страница 10

14.5. ПРИМЕНЕНИЕ МЕТОДА ЗЕРКАЛЬНЫХ ИЗОБРАЖЕНИЙ

Задача 14.27. По уединенному проводу, находящемуся вблизи гра-ницы раздела разных магнитных сред протекает постоянный ток    I= 130 А (рис. 14.37,а). Расстояние  d= 70 см,  а радиус провода очень мал по сравне-нию с d.

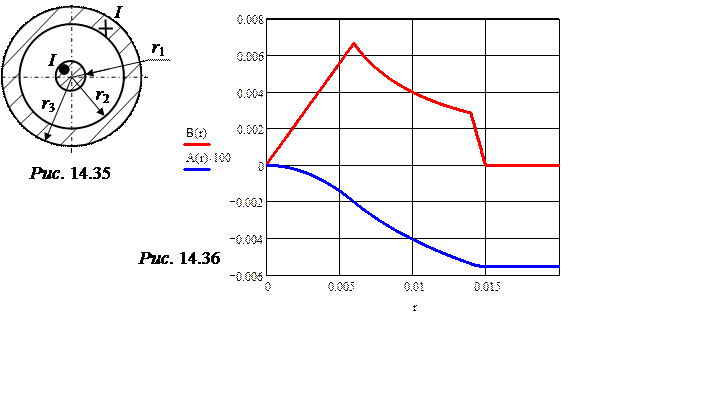
Требуется: 1) рассчитать напряженности магнитного поля в точках  А(x_A = -15 см; y_A = 30 см)  и  В(x_B = 20 см; y_B = -35 см), а также магнитное напряжение между ними; 2) считая, что А и В являются точками сечения длин-ных сторон прямоугольной рамки длиной  l = 5 м  и с числом витков  w = 200, найти магнитный поток рамки и взаимную индуктивность провода и рамки.

Решение

Поскольку провод находится вблизи границы раздела сред с различными магнитными проницаемостями, то для решения задачи применим метод зеркальных изображений, согласно которому поле в правом полупространстве может быть рассчитано согласно рис. 14.37,б, а поле в левом – согласно рис. 14.37,в.

Определим коэффициенты для фиктивных токов:

k₁ =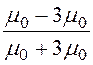= -0,5;       k₂ =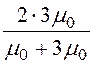= 1,5.

Тогда  I₁ = k₁I = -65 A;   I₂ = k₂I = 195 A.  В дальнейшем значение тока I₁ будем брать положительным, но его направление поменяем на противо-положное по сравнению с I, что отражено на рис. 14.37,б.

1. Расчет напряженностей.

В т. А  напряженность создается только током  I₂  (рис. 14.10,в) и определяется она в соответствии с законом полного тока:

H_A =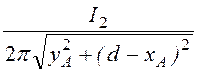==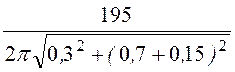 34,4 .

В т. В напряженность создается токами  I  и  I₁ (рис. 14.10,б). Вычислим проекции на оси  x и  y  составляющих  H¢_B  и  H¢¢_B:

H¢_Bx = H¢_B·cosa₁ =

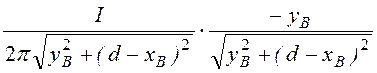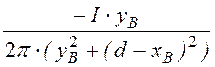=== 19,4 ;

H¢_By = H¢_B·sina₁ =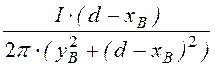= 27,77 ;

H¢¢_Bx = H¢¢_B·cosa₂ =

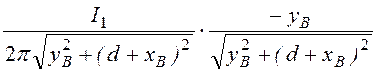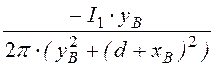=== 3,88 ;

H¢¢_By = H¢¢_B·sina₂ =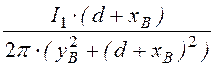= 9,99 .

Тогда     Н_Вx = Н¢_Вx – Н¢¢_Вx = 15,52 A/м;     Н_Вy = Н¢_Вy + Н¢¢_Вy = 37,76 A/м;

Н_В == 40,84 A/м.

2. Расчет магнитного напряжения.

Его произведем методом наложения. Составляющая напряжения, создаваемая токами  I  и  I₂ (см. рис. 14.37) в соответствии с (14.4)

U_mAB¢ =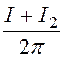(a₁ + b₁), где  a₁ и b₁ – выраженные в радианах углы, показанные на рис. 14.37,в.

a₁= arctg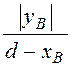= 0,61;  b₁ = arctg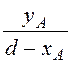= 0,34;

U_mAB¢ =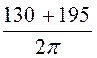(0,61 + 0,34) = 49,14 A.

Составляющая  U_mAB¢¢, создаваемая током  I₁ (рис. 14.37,б),

U_mAB¢¢ =(a₂ + g₁),     a₂ = arctg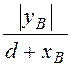= 0,371;  g₁ = arctg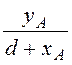= 0,5;

U_mAB¢¢ =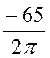(0,371 + 0,5) = -9 A.

Тогда      U_mAB = U_mAB¢ + U_mAB¢¢ = 40,14 A.

3. Расчет магнитного потока.

Поскольку части рамки находятся в разных средах, то используем промежуточную точку D, у которой (рис. 14.37,в)

y_D = y_A – x_A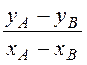= 0,021 м.

Тогда составляющая магнитного потока в той части рамки, которая находится в левом полупространстве в соответствии с (14.3)

Ф¢ =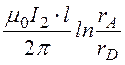==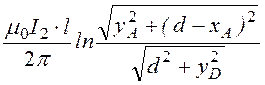 4,92·10 ^-5 Вб.

Составляющая магнитного потока в той части рамки, которая находится в правом полупространстве

Ф¢¢ =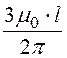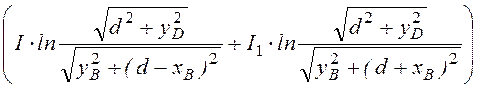= 1,16·10 ^-4 Вб.

Магнитный поток через рамку     Ф = Ф¢+ Ф¢¢ = 1,65·10 ^-4 Вб.

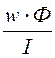Взаимная индуктивность провода и рамки    М = = 2,55·10 ^-4 Гн.

Задача 14.28. Плоская шина с током  I= 500 А  расположена вблизи границы раздела различных магнитных сред (рис. 14.38,а) на расстоянии       а = 5 мм  от границы. Требуется определить магнитную индукцию в точке А и взаимную индуктивность шины и прямоугольной рамки, содержащей         w = 200 витков.

Решение

Для решения задачи применим метод зеркальных изображений. Определим коэффициенты для фиктивных токов:

k₁ =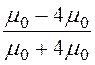= -0,6;     k₂ =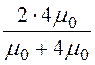= 1,6.

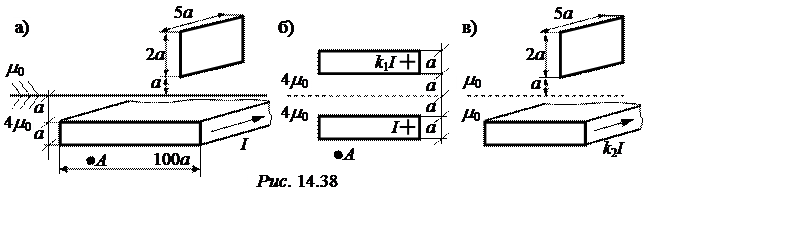
Тогда магнитное поле в нижнем полупространстве рассчитаем согласно рис. 14.38,б. Поскольку ширина шины намного больше её толщины, то можно пренебречь краевым эффектом и в соответствии с законом полного тока, а также методом наложения напряженность поля и индукция в точке А:

Н_А =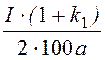==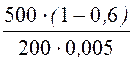 200 А/м;   В_А = 4m₀Н_А = 1,0·10 ^-3 Тл.

Взаимная индуктивность провода и рамки  М =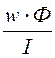, где  Ф – магнитный поток, сцепленный с витками рамки. Его расчет произведем по рис. 14.38,в:

Ф = S·m₀Н = 2а∙5а∙m₀∙k₂∙I/(2∙100a).

Тогда  М= 10а∙m₀∙k₂∙w/200 = 0,10∙10 ^-6  Гн.