Магнитное поле. Основные теоретические положения, страница 6

Магнитное   напряжение   между   произвольными   точками   Е   и   G: U_mЕG =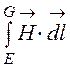. В областях, не занятых проводниками, магнитное поле является потенциальным, следовательно, магнитное напряжение не зависит от путей интегрирования, если они не образуют контуров, связанных с токами. Поэтому нужно выбрать путь интегрирования ЕG таким, чтобы вычисление интеграла было простым – вдоль радиальных линий и по окружности. Таким образом,

U_mЕG = U_mЕF + U_mFG = -·b + 0 = -·b.

Выводы. 1. Точки, лежащие на радиальной к проводнику линии, имеют один и тот же потенциал, то есть радиальная линия является эквипотенциалью.

2. Магнитное напряжение зависит от угла между точками и не зависит от расстояния от них до провода. Напряжение для произвольной кривой  LN вычисляется по формуле

U_mLN = ±·g;                                     (14.4)

здесь g – выраженный в радианах угол, под которым дуга LN видна из центра проводника.

3. Если интегрирование осуществляется вдоль силовых линий, магнитное напряжение положительно, если против – отрицательно.

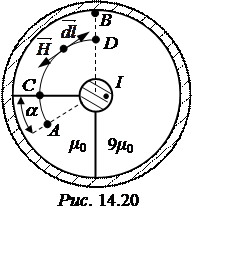
ЗАДАЧА 14.18. По жиле коаксиального кабе-ля (рис. 14.20) протекает ток   I= 360 А.  Определить магнитное напряжение между точками А и B, если   a= 30°.

Решение

Магнитное напряжение между точками А и В определим по формуле  U_mAB =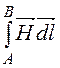. путь движения выберем А-С-D-В (рис. 14.20), учитывая, что из-за различных магнитных проницаемостей сред напряженности в них разные. Тогда

U_mAB =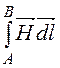=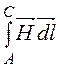++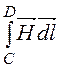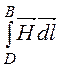= -Н₁·l_AC – Н₂·l_CD, где  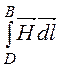  = 0  из-за перпендикулярности векторов    и  ;

  и   –  напряженности в областях с  m₀  и  9m₀,  соответственно;

напряжения Н·l взяты с минусом, поскольку направления векторов        и   противоположные.

Величины Н₁ и Н₂ определим с помощью закона полного тока

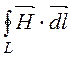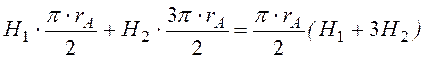== I.

В силу того, что нормальная составляющая вектора  на границе раздела двух сред непрерывна, имеем

m₀Н₁ = 9m₀Н₂.

Решая совместно два последних уравнения, получаем

Н₁ =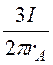;    Н₂ =.

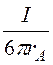Учитывая, что  l_AC = r_A·a,  где a должно быть выражено в радианах, и  l_CD = r_A·,  получаем

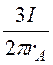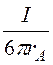U_mAB = -Н₁·l_AC – Н₂·l_CD = -·r_A·–·r_A·== -120 A.

Задача 14.19. Уединённый провод с током   I = 10 А   находится  на границе раздела сред (рис. 14.21):  m₁ = 2,   m₂ = 4,   m₃ = 6.   Координаты точек  х_А = у_А = 10 см,    х_В = -5 см,   у_В = -15 см.  Требуется:

1. 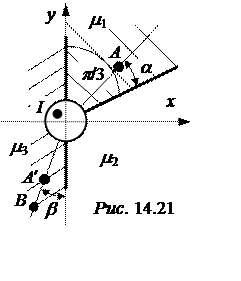 Рассчитать напряжённости магнитного поля в точках А и В, а также магнитное напряжение между ними.

2. Считая, что А и В являются точками сечения длинных сторон прямоугольной рамки длиной   l = 1 м  и с числом витков w = 100,  найти магнитный поток рамки и взаимную индуктивность провода и рамки.

Решение

Вычислим расстояния от центра провода до точек А и В:

r_A = 10= 14,14 см,   r_B == 15,81 см.

Для расчета напряжённости магнитного поля в точке А проведём через неё окружность с центром, совпадающим с осью провода. На основании закона полного тока можно записать:

H₁·r_A + H₂·r_A + H₃·p ·r_A = I, где  H₁,  H₂,  H₃ –  напряженность поля в среде с проницаемостью, соответ-ственно,  m₁, m₂, m₃.

Границы расположены радиально, поэтому векторы  и  на границе имеют только нормальную составляющую. Граничное условие  В_1n = В_2n = В_3n, откуда  m₁·H₁ = m₂·H₂ = m₃·H₃.

Таким образом,    H₁·(r_A +·r_A +·pr_A) = I,  откуда

H_А = H₁ = I/(r_A +·r_A +·pr_A) =

= 10·3/((1+0,5·2+1/3·3)·p ·0,1414) = 22,51 А/м.

Аналогично, напряжённость в точке В:

H_В = H₃ =H₁ =I/(r_В +·r_В +·pr_В) =

= 10/((1+0,5·2+1/3·3)·p ·0,1581) = 6,71 А/м.

магнитное напряжение между точками А и В при движении по часовой стрелке (против силовых линий) можно вычислить по формуле (см. зад. 14.18):     U_mAB = -H₁·r_A·a – H₂·r_A·– H₃·r_A·b;

H₁·r_A = 30/(3p),    H₂·r_A = 15/(3p),   H₃·r_A = 10/(3p),

a = – arctg= – = рад,   b = arctg= arctg= 0,3218 рад.

Таким образом,    U_mAB = -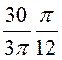––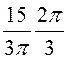·0,3218 = -5,24 А.